Yksinkertainen Autorange -kondensaattorimittari / kapasitanssimittari Arduinolla ja käsin: 4 vaihetta

2024 Kirjoittaja: John Day | [email protected]. Viimeksi muokattu: 2024-01-30 09:01

Hei!

Tätä fysiikkayksikköä varten tarvitset:

* virtalähde 0-12V

* yksi tai useampi kondensaattori

* yksi tai useampi latausvastus

* sekuntikello

* yleismittari jännitteen mittaamiseen

* arduino nano

* 16x2 I²C -näyttö

* 1 / 4W vastukset 220, 10k, 4,7M ja 1Gohms 1 gohms vastuksella

* dupont -lanka

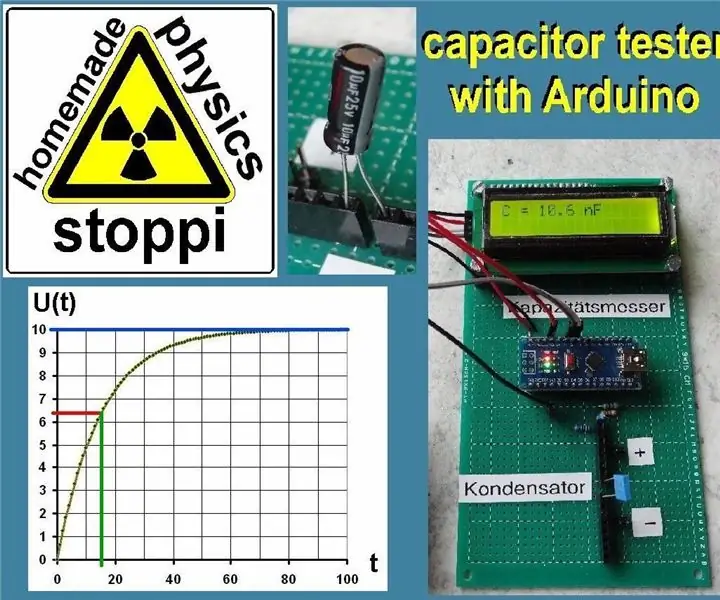
Vaihe 1: Yleistä kondensaattoreista

Kondensaattoreilla on erittäin tärkeä rooli elektroniikassa, niitä käytetään varausten tallentamiseen suodattimena, integraattorina jne. Mutta matemaattisesti kondensaattoreissa on paljon. Joten voit harjoitella eksponentiaalisia toimintoja kondensaattoreilla ja heillä. treenata. Jos alun perin varaamaton kondensaattori on kytketty vastuksen kautta jännitelähteeseen, varaukset virtaavat jatkuvasti kondensaattoriin. Kun varaus Q kasvaa, kaavan Q = C * U (C = kondensaattorin kapasitanssi) mukaan myös jännite U kondensaattorin poikki kasvaa. Latausvirta pienenee kuitenkin yhä enemmän, kun nopeasti ladattu kondensaattori on yhä vaikeampi täyttää varauksilla. Kondensaattorin jännite U (t) noudattaa seuraavaa kaavaa:

U (t) = U0 * (1-exp (-k * t))

U0 on virtalähteen jännite, t on aika ja k on latausprosessin nopeuden mitta. Mistä kooista k riippuu? Mitä suurempi tallennuskapasiteetti (eli kondensaattorin kapasitanssi C), sitä hitaammin se täyttyy varauksilla ja hitaammin jännite kasvaa. Mitä suurempi C, sitä pienempi k. Kondensaattorin ja virtalähteen välinen vastus rajoittaa myös varauksen siirtoa. Suurempi vastus R aiheuttaa pienemmän virran I ja siten vähemmän varauksia sekunnissa, jotka virtaavat kondensaattoriin. Mitä suurempi R, sitä pienempi k. Oikea suhde k: n ja R: n tai C: n välillä on:

k = 1 / (R * C).

Jännite U (t) kondensaattorissa kasvaa siten kaavan U (t) = U0 * (1-exp (-t / (R * C)))

Vaihe 2: Mittaukset

Oppilaiden tulee syöttää jännite U aikaan t taulukkoon ja piirtää sitten eksponenttifunktio. Jos jännite kasvaa liian nopeasti, sinun on lisättävä vastusta R. Toisella puolella, jos jännite muuttuu liian hitaasti, vähennä R: tä.

Jos tiedetään U0, vastus R ja jännite U (t) tietyn ajan t kuluttua, kondensaattorin kapasitanssi C voidaan laskea tästä. Tätä varten yhtälö on logaritmoitava ja joidenkin muunnosten jälkeen saadaan: C = -t / (R * ln (1 - U (t) / U0))

Esimerkki: U0 = 10 V, R = 100 kohmia, t = 7 sekuntia, U (7 sekuntia) = 3,54 V. Sitten C johtaa arvoon C = 160 μF.

Mutta on toinen, yksinkertainen menetelmä kapasiteetin C määrittämiseksi. Nimittäin jännite U (t) t = R * C jälkeen on täsmälleen 63,2% U0: sta.

U (t) = U0 * (1-exp (-R * C / (R * C)) = U0 * (1-exp (-1)) = U0 * 0,632

Mitä tämä tarkoittaa? Opiskelijoiden on määritettävä aika t, jonka jälkeen jännite U (t) on täsmälleen 63,2% U0: sta. Erityisesti yllä olevassa esimerkissä etsitään aikaa, jonka jälkeen jännite kondensaattorin yli on 10 V * 0,632 = 6,3 V. Näin on 16 sekunnin kuluttua. Tämä arvo lisätään nyt yhtälöön t = R * C: 16 = 100000 * C. Tämä antaa tuloksen: C = 160 μF.

Vaihe 3: Arduino

Harjoituksen lopussa kapasiteetti voidaan määrittää myös Arduinolla. Tämä laskee kapasiteetin C täsmälleen aikaisemman menetelmän mukaisesti. Se lataa kondensaattorin tunnetun vastuksen R kautta 5 V: lla ja määrittää ajan, jonka jälkeen jännite kondensaattorissa = 5 V * 0,632 = 3,16 V. Arduino-digitaali-analogimuunnin 5V on 1023. Siksi sinun tarvitsee vain odottaa, kunnes analogiatulon arvo on 1023 * 3,16 / 5 = 647. Tällä kertaa kapasiteetti C voidaan laskea. Jotta voidaan mitata kondensaattoreita, joilla on hyvin erilainen kapasitanssi, käytetään 3 eri latausvastusta. Ensinnäkin matalaa vastusta käytetään latausajan määrittämiseen aina 647. asti. Jos tämä on liian lyhyt, eli jos kondensaattorin kapasitanssi on liian pieni, valitaan seuraava suurempi latausvastus. Jos tämä on myös liian pieni, 1 Gohms -vastus seuraa mittauksen lopussa. C -arvo näytetään sitten näytöllä oikealla yksiköllä (µF, nF tai pF).

Vaihe 4: Johtopäätökset

Mitä opiskelijat oppivat tässä yksikössä? Opit kondensaattoreista, niiden kapasitanssista C, eksponentiaalisista funktioista, logaritmista, prosenttilaskelmista ja Arduinosta. Ajattelen paljon.

Tämä laite sopii 16-17-vuotiaille opiskelijoille. Olet varmasti käynyt läpi eksponentiaalisen funktion ja matematiikan logaritmin. Hauskaa kokeilua luokallasi ja Eurekalla!

Olisin erittäin iloinen, jos äänestäisitte minua luokkahuoneen tiedekilpailussa. Kiitos paljon tästä!

Jos olet kiinnostunut muista fysiikkaprojekteistani, tässä on youtube -kanavani:

lisää fysiikkahankkeita: