
Sisällysluettelo:
- Vaihe 1: Mikä on AD -muunnin?
- Vaihe 2: Käytetyt resurssit
- Vaihe 3: ESP32 ADC
- Vaihe 4: Käytetty piiri
- Vaihe 5: Merkki käytetty
- Vaihe 6: Oskilloskoopin hankkimat tiedot
- Vaihe 7: Oskilloskoopin hankkimat tiedot (csv -tiedosto Excelissä)
- Vaihe 8: ADC: n hankkimat tiedot
- Vaihe 9: ADC: n hankkimat tiedot - Excel
- Vaihe 10: Kiipeilyramppien vertailu
- Vaihe 11: Näytteiden lukumäärän vastaaminen
- Vaihe 12: Aukkojen täyttäminen - trendirivi
- Vaihe 13: Aukkojen täyttäminen - Grade 2 -polynomikäyrä
- Vaihe 14: Aukkojen täyttäminen - toiminnon arviointi
- Vaihe 15: Oskilloskoopin jännitteen muuntaminen vastaavaan arvoon verrattuna ADC: hen
- Vaihe 16: Kahden saavutetun rampin vertailu
- Vaihe 17: ADC Reading Difference (ERROR) -käyttäytyminen
- Vaihe 18: ADC -lukujen erokäyttäytyminen - korjaustoiminnon löytäminen
- Vaihe 19: Muiden ohjelmistojen käyttäminen
- Vaihe 20: Vakiot ja asetukset ()
- Vaihe 21: Silmukka () ja korjaustoiminto
- Vaihe 22: PolySolve Correction -toiminnon käyttäminen
- Vaihe 23: Tallenna korjauksella - Plotter -sarja
- Vaihe 24: Laskennalliset kustannukset
- Vaihe 25: Testikoodi - Asennus () ja silmukan käynnistys ()
- Vaihe 26: Testikoodi - silmukka () ja käsittely
- Vaihe 27: Testikoodi - silmukka () - Tulokset
- Vaihe 28: Testikoodi - käytetyt toiminnot
- Vaihe 29: Tiedostot
- Kirjoittaja John Day day@howwhatproduce.com.
- Public 2024-01-30 09:02.
- Viimeksi muokattu 2025-01-23 14:43.
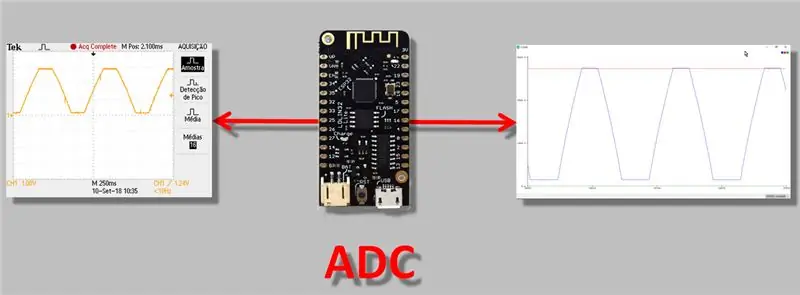


Tänään aion puhua teknisemmästä ongelmasta, mutta mielestäni kaikkien, jotka työskentelevät ESP32: n kanssa, pitäisi tietää: ADC (analoginen-digitaalinen muunnin) -lukujen säätö. Pidän tätä tärkeänä, koska kun teet "mittausta", etenkin jos laitteella on analoginen lähtö, sinun on oltava täysin varma, että lukema suoritetaan oikein.
Tämän päivän videossa teemme siis mittauksia ESP32: n "analoginen-digitaalinen muunnin" -laitteella, tarkkailemme muunnoseroja ja käytämme ADC-säätö- / kalibrointimenetelmää.
Vaihe 1: Mikä on AD -muunnin?
AD -muunnin on piiri, joka pystyy muuntamaan analogisen (jatkuvan) määrän digitaaliseksi (diskreetiksi). Mitä tuo tarkoittaa? Se tarkoittaa, että vaikka digitaaliset arvot voivat olettaa vain erillisiä arvoja, jotka muodostuvat nollien ja ykkösten yhdistelmästä, analoginen määrä voi olettaa mitä tahansa arvoa alueella. Jos esimerkiksi mittaamme ihanteellisen AA -kennon jännitteen, voimme löytää minkä tahansa arvon välillä 0V - 1,5V, koska tämä on analoginen määrä. Ihanteellisen lampun lähtötilan on oletettava vain kaksi tilaa (pois päältä tai päällä), mikä on diskreetti suuruus. Koska mikro -ohjaimet toimivat tätä erillistä logiikkaa käyttäen, tarvitsemme piirin, joka pystyy kääntämään analogisen määrän digitaaliseksi (tai diskreetiksi).
Vaihe 2: Käytetyt resurssit
• Yksi Lolin32 Lite -kortti v1.0.0
• Tektronix TDS1001C -oskilloskooppi kuvaamiseen
• Yksi USB -kaapeli ESP32: lle
• Hantek DSO4102C -oskilloskooppi signaaligeneraattorina
Vaihe 3: ESP32 ADC

Espressifin tietojen mukaan ESP32-siruissa voi olla +/- 6% ero sirusta toiseen mitatuissa tuloksissa.
Lisäksi muunnoksella EI ole lineaarista vastausta jokaiselle käytettävissä olevalle lukualueelle. Espressif tarjoaa kalibrointimenetelmän ja ehdottaa, että käyttäjät ottavat käyttöön muita menetelmiä, jos he pitävät sitä tarpeellisena halutun tarkkuuden saavuttamiseksi.
Suoritamme tietojen keräämisen ja näytämme tästä ADC -vastaukset ja esimerkin matemaattisen prosessin soveltamisesta säädön lukemiseen.
On olemassa useita (yksinkertaisempia tai monimutkaisempia) tapoja tehdä nämä korjaukset. Sinun tehtäväsi on arvioida projektillesi sopivin.
Tässä esitetyllä on havainnollistava tarkoitus ja se pyrkii käsittelemään mielenkiintoisia kohtia, jotka voidaan havaita säätöjen aikana.
Vaihe 4: Käytetty piiri
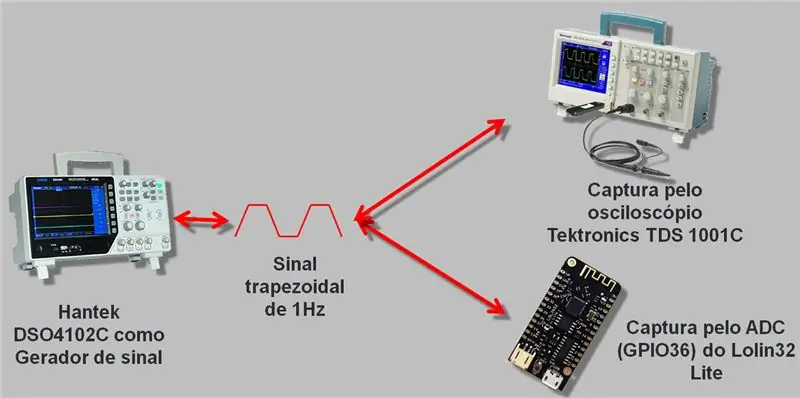
Käytin oskilloskooppia ja signaaligeneraattoria, joka kulkee jopa 25 MHz, Hantek DSO4102C. Loimme aallon, jonka ESP A / D ja oskilloskooppi lukivat. Kerätyt tiedot tallennettiin csv -muodossa ja laskentataulukkoon, jonka jätän artikkelin loppuun ladattavaksi.
Vaihe 5: Merkki käytetty
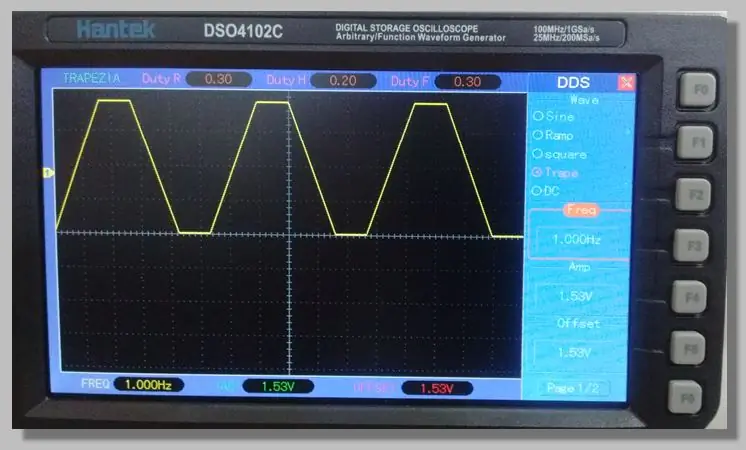
Valitsimme matalataajuisen puolisuunnikkaan signaalin, joka mahdollistaa pääsyn koko muunnosalueen läpi kulkeville rampeille. Tämä mahdollistaa suuren määrän näytteitä näillä rampeilla.
Vaihe 6: Oskilloskoopin hankkimat tiedot
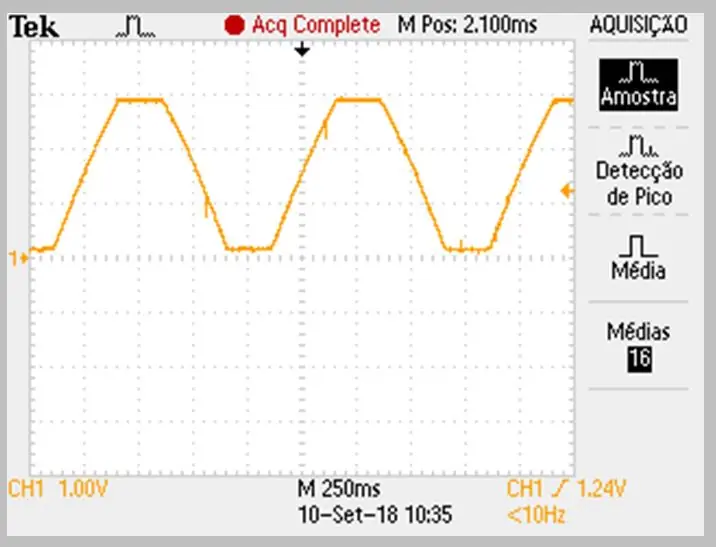
Kuva kaappauksesta suoritettiin oskilloskoopilla. Tiedot tallennettiin csv -tiedostoon. Huomaa pieni kaarevuus signaalin nousu- ja laskurampeissa.
Vaihe 7: Oskilloskoopin hankkimat tiedot (csv -tiedosto Excelissä)
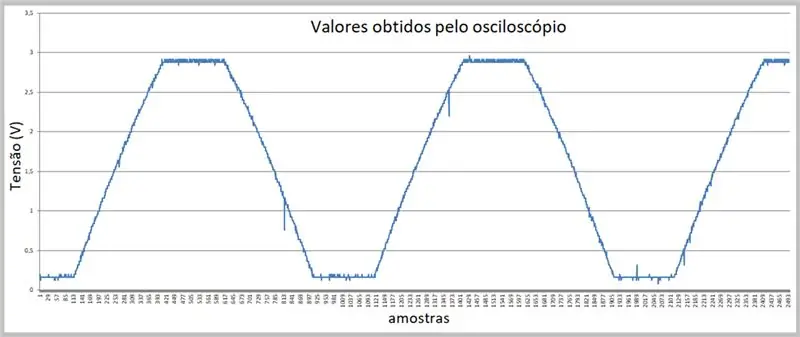
Meillä on näytteitä täällä.
Vaihe 8: ADC: n hankkimat tiedot
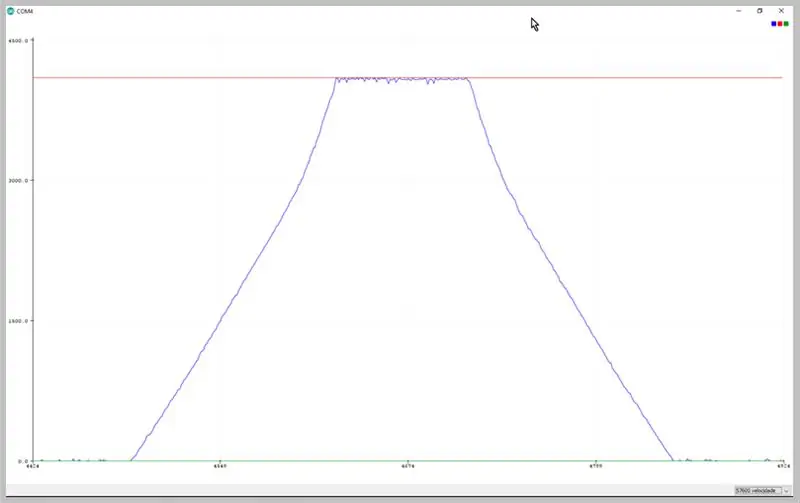
Muuttamalla sarjan siirtonopeutta voimme tarkastella ADC: n sieppaamia tietoja. Tarkkaile puolisuunnikkaan signaalin muodonmuutosta.
Tiedot havaittiin Arduino IDE -sarjaplotterissa
Vaihe 9: ADC: n hankkimat tiedot - Excel
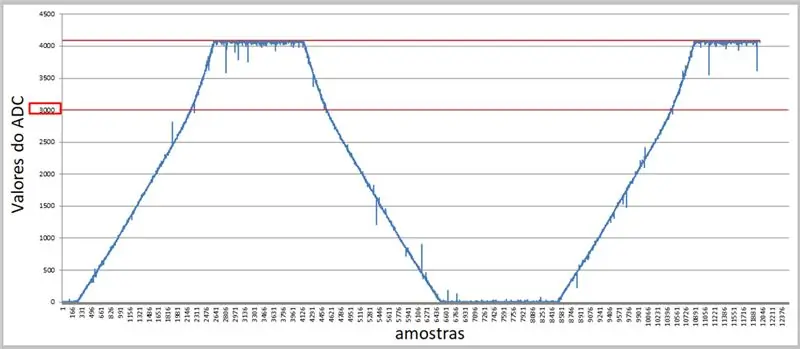
Korkeamman nopeuden ja sarjapäätteen avulla voimme kaapata arvot ja soveltaa niitä Excelissä vertailuja varten.
Vaihe 10: Kiipeilyramppien vertailu
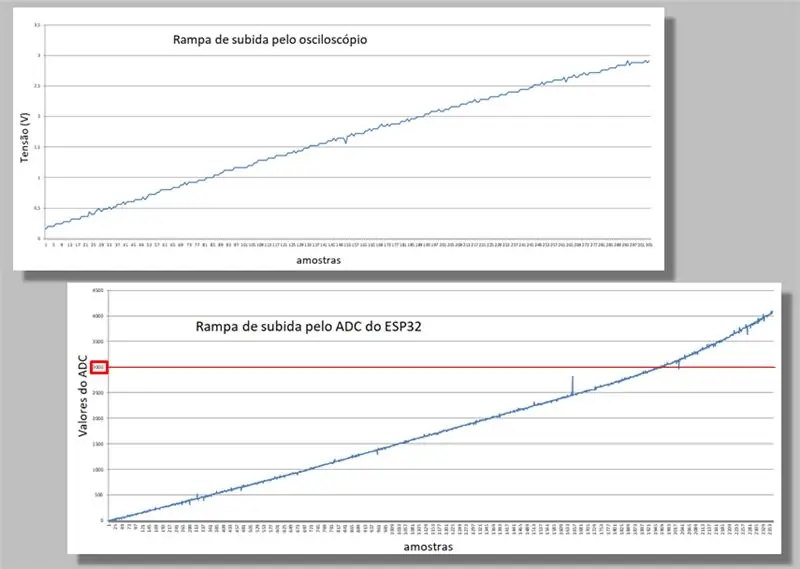
Vertaamme kahden saaliin kahta kiipeilyramppia.
Huomaa kummankin luiskan kaarevuus.
Huomaa myös, että samaa ramppia varten meillä on paljon enemmän ESP32 -näytteitä kuin oskilloskoopista.
Vaihe 11: Näytteiden lukumäärän vastaaminen

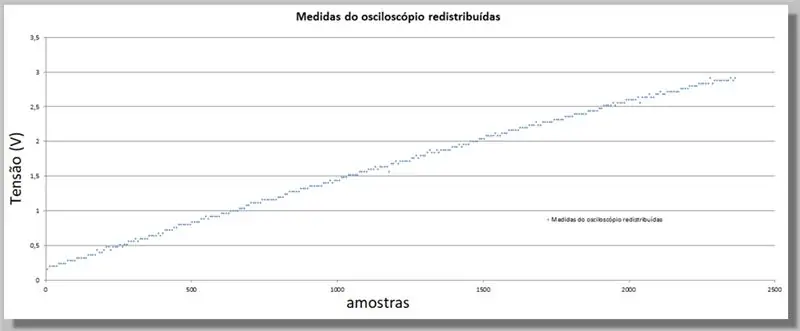
Koska ESP32 tarjosi suuremman määrän näytteitä kuin oskilloskooppi, meidän on rinnastettava nämä arvot, koska ne toimivat indeksinä kahden käyrän vertaamiseksi.
Tätä varten teemme suoran vertailun.
Meillä on 305 näytettä oskilloskoopin ramppia ja 2365 näytettä ADC -ramppia varten.
Koska luiskat ovat samaa aluetta, voimme sanoa, että meillä on noin 7,75 näytettä ADC: tä kutakin oskilloskooppia kohti.
Kunkin oskilloskooppinäytteen indeksin kertomalla on sama käyrä, mutta indeksit vastaavat ADC: tä ja uudelleenjaettuja tietoja.
Täyttääksemme puuttuvat tiedot uusista tehtävistä käytämme käyrää, joka sopii tilastollisesti tunnettuihin tietoihin.
Vaihe 12: Aukkojen täyttäminen - trendirivi
Valitsemalla tiedossa olevat tiedot (siniset pisteet) napsauttamalla ja napsauttamalla sitten oikeaa painiketta valitsemme: "Lisää trendirivi …"
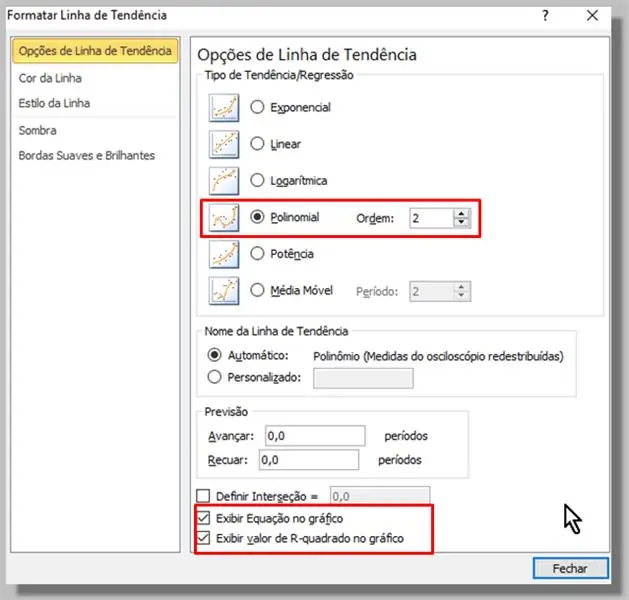
Valitsemme avautuvassa ikkunassa Polynomi -tyypin (tilaus 2 riittää).
Tarkistimme myös vaihtoehdot "Näytä yhtälö kaaviossa" ja "Näytä R-neliöarvo kaaviossa".
Napsauta "Sulje".
Vaihe 13: Aukkojen täyttäminen - Grade 2 -polynomikäyrä
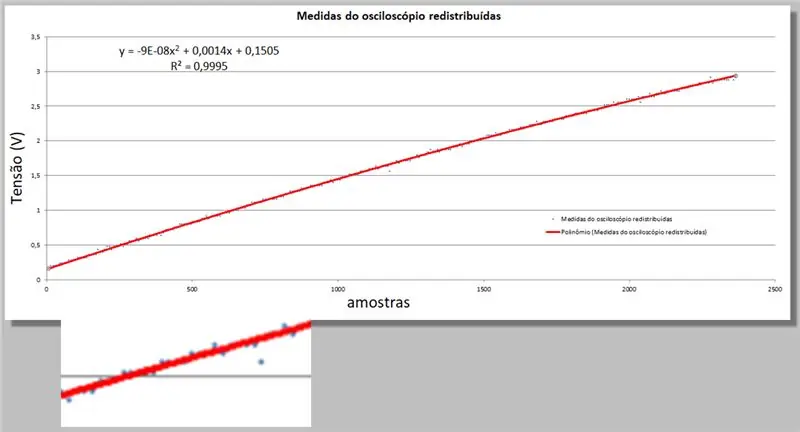
Excel antaa meille kaksi uutta tietoa; toisen kertaluvun yhtälö, joka sopii parhaiten dataan, ja R-neliöyhtälö, joka ilmaisee tämän riittävyyden.
Muista vain, että mitä lähempänä 1, sitä sopivampi yhtälö.
Älkäämme syventykö matematiikkaan, vaan käytämme sitä työkaluna.
Vaihe 14: Aukkojen täyttäminen - toiminnon arviointi
Täytetään näytteenottoaukot yhtälön tuottamilla tiedoilla. Ja sitten vertaa niitä kohta kohdalta.
y = -9E -08x2 + 0, 0014x + 0, 1505
R² = 0, 9999
Oskilloskoopin jännite = -9E -08 * indeksi2 + 0, 0014 * indeksi + 0, 1505
Vaihe 15: Oskilloskoopin jännitteen muuntaminen vastaavaan arvoon verrattuna ADC: hen

Hyödynnä tätä hyötyä muuntaaksemme myös oskilloskoopin jännitteen arvon vastaavaksi ADC -arvoksi.
Koska korkein ESP32: n ADP: ssä saatu arvo oli 4095, mikä vastaa 2,958 V: n lukemaa samalla indeksillä, voimme sanoa, että:
Kukin voltti oskilloskoopin mittauksissa vastaa noin 1384,4 AD -yksikköä. Siksi voimme kertoa kaikki oskilloskoopin mittaukset tällä arvolla.
Vaihe 16: Kahden saavutetun rampin vertailu
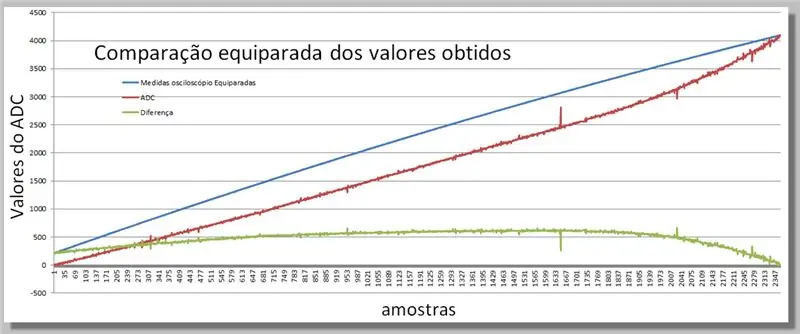
Visualisoi kahden lukeman erot.
Vaihe 17: ADC Reading Difference (ERROR) -käyttäytyminen
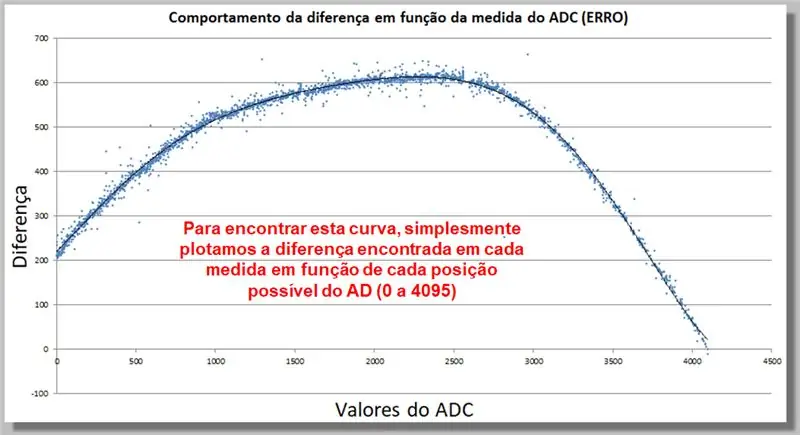
Alla oleva käyrä osoittaa, miten ADC -lukeman ero toimii mittauksen funktiona. Tämän tiedonkeruun avulla voimme löytää korjaustoiminnon.
Tämän käyrän löytämiseksi piirrämme yksinkertaisesti kussakin mittauksessa havaitun eron kunkin mahdollisen AD -sijainnin funktiona (0-4095).
Vaihe 18: ADC -lukujen erokäyttäytyminen - korjaustoiminnon löytäminen
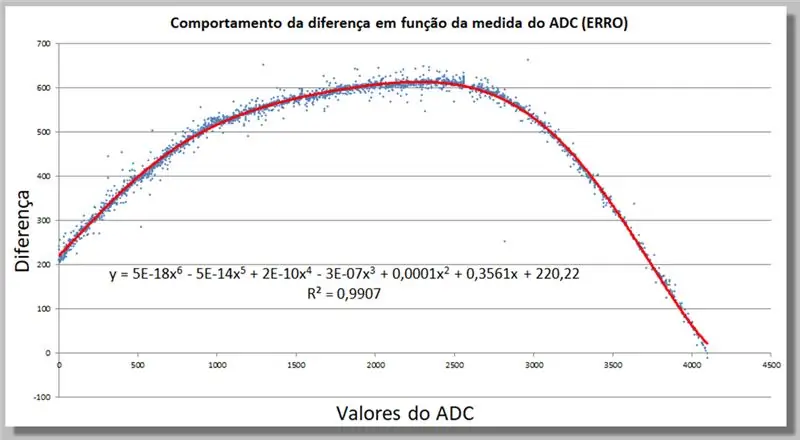
Voimme määrittää Excelissä korjaustoiminnon lisäämällä nyt korkeamman suuntauslinjan, kunnes se sopii riittävästi tietoihimme.
Vaihe 19: Muiden ohjelmistojen käyttäminen
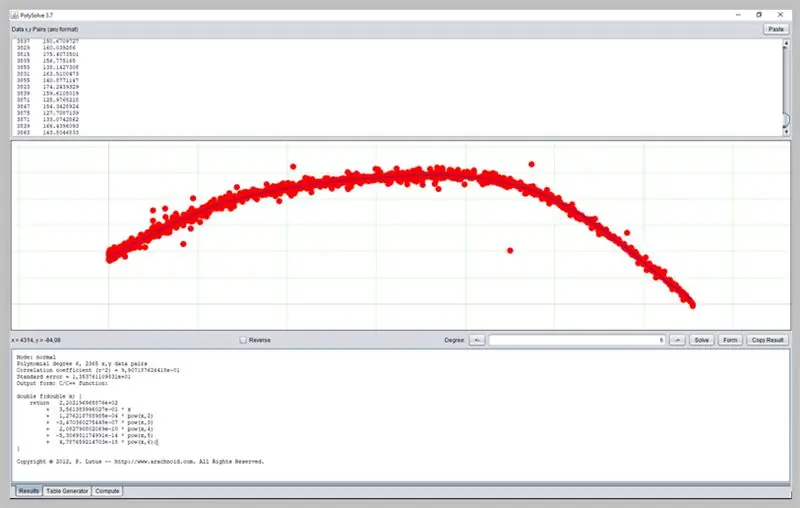
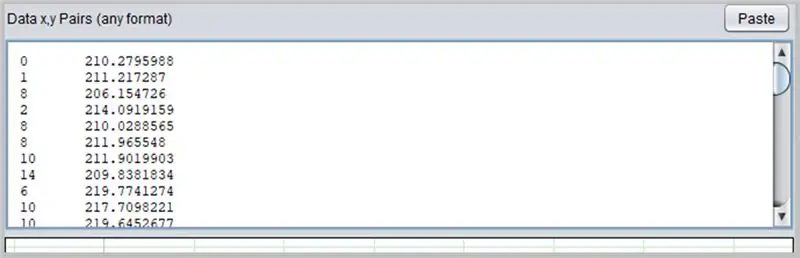
Muita mielenkiintoisia ohjelmistoja käyrien määrittämiseen on PolySolve, jota voidaan käyttää suoraan linkistä: https://arachnoid.com/polysolve/ tai ladata Java -sovelluksena.
Se mahdollistaa korkeamman asteen polynomi-regressioiden soveltamisen ja muotoillun funktion sekä muiden toimintojen toimittamisen.
Voit käyttää sitä kirjoittamalla tiedot ensimmäiseen tekstikenttään. Tietojen on noudatettava järjestystä X, Y pilkulla tai sarkaimella erotettuna. Ole varovainen käyttäessäsi pistettä oikein desimaalipisteenä.
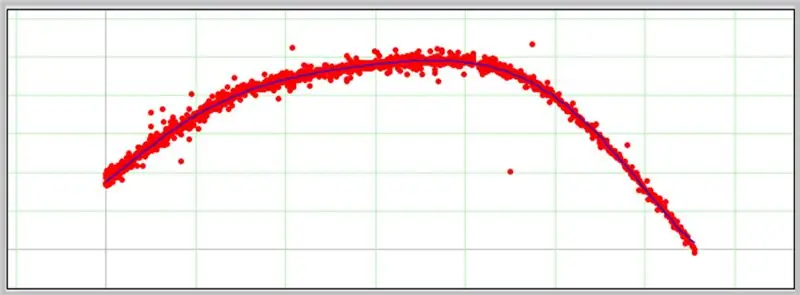
Kaavio näkyy seuraavassa ruudussa, jos syötetyt tiedot on muotoiltu oikein.
Näin ADC -virhekäyrämme meni.
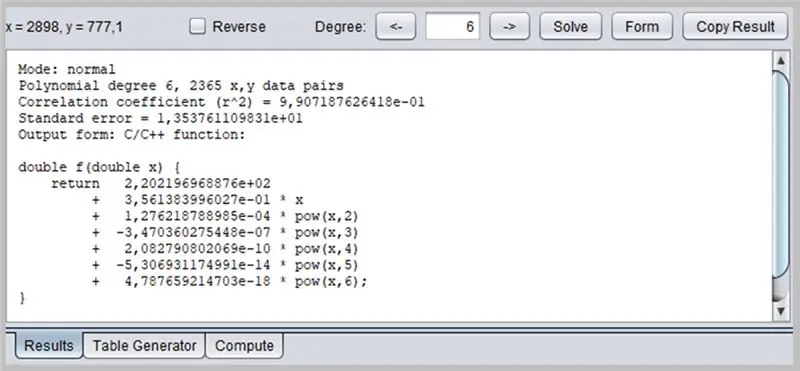
Tässä ikkunassa esitetään regression tulos, mukaan lukien toimintojen riittävyystiedot, joiden lähtö voidaan muotoilla useilla tavoilla: C / C ++ -funktiona, kertoimien luettelo, Java -funktio jne.
Huomautus: Kiinnitä huomiota desimaalierottimiin
Vaihe 20: Vakiot ja asetukset ()
Mainitsen tässä GPIO: n, jota käytettiin analogiseen sieppaukseen. Alustan sarjaportin sekä analogista sieppausta varten määritetyn nastan.
const int pin_leitura = 36; // GPIO usado para captura analógica void setup () {Serial.begin (1000000); // Iniciciando a porta serial somente para debug pinMode (pin_leitura, INPUT); // Pino utilizado para captura analógica}
Vaihe 21: Silmukka () ja korjaustoiminto
Tallennamme säädetyn jännitteen ja tulostamme arvot oikeilla korjauksilla tai ilman niitä.
void loop () {int valor_analogico = analoginenLue (pin_leitura); // realiza a captura da tensão ajustada // Serial.print(valor_analogico + f (valor_analogico)); // imprime os valores para debug (COM CORREÇÃO) Serial.print (valor_analogico); // imprimime os valores para debug (SEM CORREÇÃO) Serial.print (","); Serial.print (4095); // cria uma linha para marcar o valor máximo de 4095 Serial.print (","); Sarja.println (0); // cria uma linha para marcar o valor mínimo de 0}
Huomaa rivillä 12, että meillä on mahdollisuus tulostaa tiedot lisäämällä erotustoiminto f (analoginen_arvo).
Vaihe 22: PolySolve Correction -toiminnon käyttäminen
Tässä käytämme PolySolve -toimintoa Arduino IDE: n sisällä.
/* Tila: normaali Polynomi-aste 6, 2365 x, y-dataparit Korrelaatiokerroin (r^2) = 9, 907187626418e-01 Vakavirhe = 1, 353761109831e+01 Tulostusmuoto: C/C ++ -toiminto: Copyright © 2012, P. Lutus - https://www.arachnoid.com. Kaikki oikeudet pidätetään. */ double f (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2.082790802069e- 10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }
Huomaa pilkku-piste-muutos desimaalierottimena.
Vaihe 23: Tallenna korjauksella - Plotter -sarja
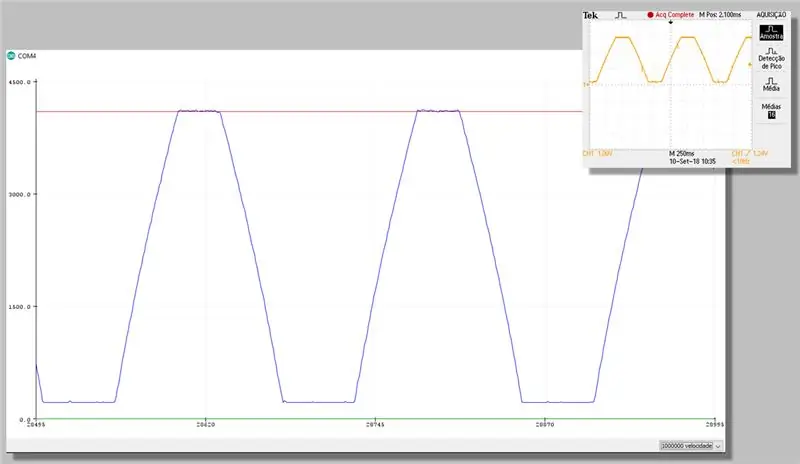
Vaihe 24: Laskennalliset kustannukset

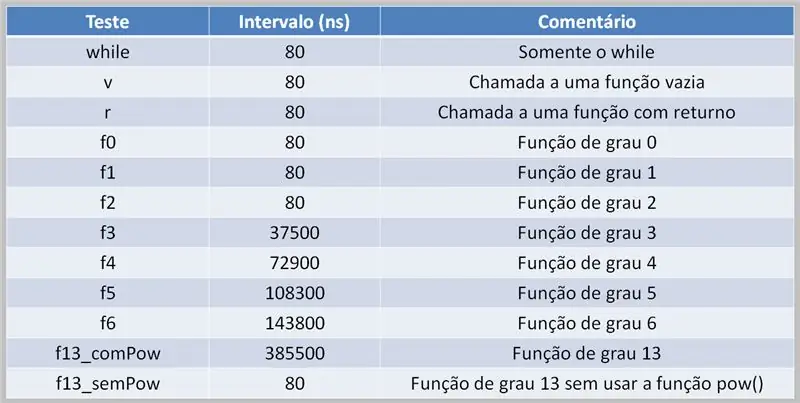
Suorittaakseen polynomilaskelmat prosessorin on suoritettava tämä tehtävä. Tämä voi johtaa suorituksen viivästymiseen lähdekoodista ja käytettävissä olevasta laskentatehosta riippuen.
Tässä näemme tuloksen taulukon testistä, jossa käytetään moniasteisia polynomeja. Huomaa ero aikojen välillä, jolloin pow () -toimintoa käytettiin ja milloin sitä ei käytetty.
Vaihe 25: Testikoodi - Asennus () ja silmukan käynnistys ()
Tässä meillä on testissä käytetty koodi.
void setup () {Serial.begin (1000000); // Iniciando a porta serial somente para debug} void loop () {float valor_analogico = 500.0; // um valor arbtrario float quantidade = 10000,0; // quantidade de chamadas float contador = 0,0; // contador de chamadas
Vaihe 26: Testikoodi - silmukka () ja käsittely
Käytin micros () -funktiota arvon saamiseksi mikrosekunneissa.
// ============= inicia o prosesso float agora = micros (); // marca o instante inicial while (contador <quantidade) {// v (valor_analogico); // função vazia // r (valor_analogico); // função com retorno // f0 (valor_analogico); // grau 0 // f1 (valor_analogico); // grau 1 // f2 (valor_analogico); // grau 2 // f3 (valor_analogico); // grau 3 // f4 (valor_analogico); // grau 4 // f5 (valor_analogico); // grau 5 // f6 (valor_analogico); // grau 6 // f13_semPow (valor_analogico); // grau 13º SEM a função POW // f13_comPow (valor_analogico); // grau 13º COM a função POW contador ++; } agora = (micros () - agora) / quantidade; // determina o intervalo que se passou para cada iteração // ============= finaliza o processo
Vaihe 27: Testikoodi - silmukka () - Tulokset
Tulostamme luokan 13 toiminnosta palautetun arvon POW: lla ja ilman vertailua sekä käsittelyvälin.
// imprime o valor retornado da função de grau 13 com e sem POW para comparação Serial.print (f13_semPow (valor_analogico)); // grau 13º SEM a função POW Serial.print (" -"); Serial.print (f13_comPow (valor_analogico)); // grau 13º COM a função POW Serial.print (" -"); // imprime o intervalo do processamento Serial.println (agora, 6); }
Vaihe 28: Testikoodi - käytetyt toiminnot
Tyhjät toiminnot (vain palauttamisen yhteydessä) asteet 0 ja 1.
// FUNÇÃO VAZIAdouble v (double x) {} // FUNÇÃO SOMENTE COM RETORNO double r (double x) {return x; } // FUNÇÃO DE GRAU 0 double f0 (double x) {return 2.202196968876e+02; } // FUNÇÃO DE GRAU 1 double f1 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x; }
Luokkien 2, 3 ja 4 toiminnot.
// FUNÇÃO DE GRAU 2double f2 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2); } // FUNÇÃO DE GRAU 3 double f3 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)); } // FUNÇÃO DE GRAU 4 double f4 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2,082790802069e-10 * pow (x, 4); }
Luokan 5 ja 6 toiminnot.
// FUNÇÃO DE GRAU 5double f5 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3) + 2,082790802069e-10 * pow (x, 4) + -5,306931174991e-14 * pow (x, 5); } // FUNÇÃO DE GRAU 6 double f6 (double x) {return 2.202196968876e + 02 + 3.561383996027e-01 * x + 1.276218788985e-04 * pow (x, 2) + -3.470360275448e-07 * pow (x, 3)) + 2.082790802069e-10 * pow (x, 4) + -5.306931174991e-14 * pow (x, 5) + 4.787659214703e-18 * pow (x, 6); }
Luokan 13 toiminto POW: n avulla.
// FUNÇÃO DE GRAU 13 USANDO O POWdouble f13_comPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * pow (x, 2) + -3, 968558178426e-06 * pow (x, 3) + 1, 047910519933e-08 * pow (x, 4) + -1, 479271312313e-11 * pow (x, 5) + 1, 220894795714e-14 * pow (x, 6) + -6, 136200785076e-18 * pow (x, 7) + 1, 910015248179e-21 * pow (x, 8) + -3, 566607830903e-25 * pow (x, 9) + 5, 000280815521e-30 * pow (x, 10) + 3, 434515045670e-32 * pow (x, 11) + -1, 407635444704e-35 * pow (x, 12) + 9, 871816383223e-40 * pow (x, 13); }
Luokan 13 toiminto ilman POW: ta.
// FUNÇÃO DE GRAU SEM USAR O POWdouble f13_semPow (double x) {return 2, 161282383460e + 02 + 3, 944594843419e-01 * x + 5, 395439724295e-04 * x * x + -3, 968558178426e-06 * x * x * x + 1, 047910519933e-08 * x * x * x * x + -1, 479271312313e-11 * x * x * x * x * x + 1, 220894795714e-14 * x * x * x * x * x * x + -6, 136200785076e-18 * x * x * x * x * x * x * x + 1, 910015248179e-21 * x * x * x * x * x * x * x * x + -3, 566607830903e- 25 * x * x * x * x * x * x * x * x * x + 5, 000280815521e-30 * x * x * x * x * x * x * x * x * x * x + 3, 434515045670e- 32 * x * x * x * x * x * x * x * x * x * x * x + -1, 407635444704e -35 * x * x * x * x * x * x * x * x * x * x * x * x + 9, 871816383223e-40 * x * x * x * x * x * x * x * x * x * x * x * x * x; }
Vaihe 29: Tiedostot
Lataa tiedostot:
INO
Laskentataulukko
Suositeltava:
Kuinka tehdä ADC: n nykyinen tunne: 5 vaihetta
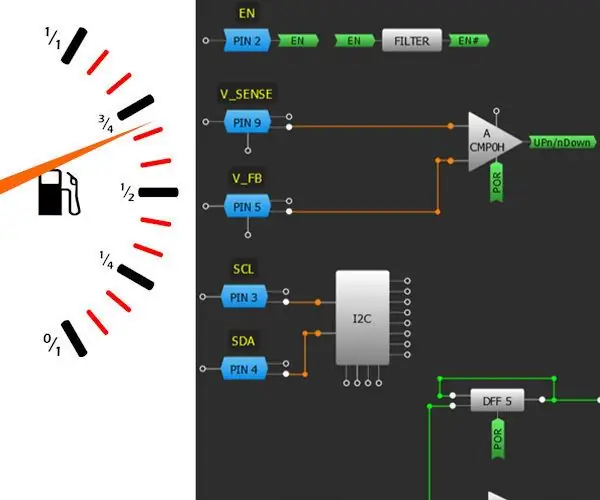
Kuinka tehdä ADC: n nykyinen järki: Tässä opastettavassa kuvataan, miten SLG46855V: ssä voidaan ottaa käyttöön 8-bittinen analogia-digitaalimuunnin (ADC), joka voi havaita kuormitusvirran ja rajapinnan MCU: n kanssa I2C: n kautta. Tätä mallia voidaan käyttää erilaisiin virranmittaussovelluksiin, kuten
Tiedätkö, miltä kasveistasi tuntuu? [Partikkeli+Ubidot]: 6 vaihetta
![Tiedätkö, miltä kasveistasi tuntuu? [Partikkeli+Ubidot]: 6 vaihetta Tiedätkö, miltä kasveistasi tuntuu? [Partikkeli+Ubidot]: 6 vaihetta](https://i.howwhatproduce.com/images/009/image-24561-j.webp)
Tiedätkö, miltä kasveistasi tuntuu? [Particle+Ubidots]: Mikään ei korvaa kävelyä ja maaperän käsittelyä itse, mutta nykytekniikka on mahdollistanut maaperän etävalvonnan ja inhimillisten aistieni mittaamattomien parametrien seurannan. SHT10: n kaltaiset maaperäanturit ovat nyt erittäin tarkkoja ja tarjoavat
7-segmentti näyttää ADC #Arduino-arvot, #Arduino: 4 vaihetta

7-segmentti näyttää ADC #Arduino Arvot, #Arduino: Tässä artikkelissa teen projektin, joka liittyy edelleen edelliseen artikkeliin. Nimittäin ADC -tietojen käsittely. Joten et tarvitse sarjamonitoria nähdäksesi ADC -tietojen arvon. Tässä artikkelissa teen ADC -arvon katseluohjelman. niin et
ESP32: n käytön aloittaminen - ESP32 -levyjen asentaminen Arduino IDE: hen - ESP32 vilkkuva koodi: 3 vaihetta

ESP32: n käytön aloittaminen | ESP32 -levyjen asentaminen Arduino IDE: hen | ESP32 Blink Code: Tässä ohjeessa näemme, kuinka aloittaa työskentely esp32: n kanssa ja miten asennetaan esp32 -levyt Arduino IDE: hen, ja ohjelmoimme esp 32: n suorittamaan vilkkuva koodi käyttämällä arduino ide
ESP32: Tiedätkö mitä DAC on?: 7 vaihetta

ESP32: Tiedätkö mitä DAC on ?: Tänään puhumme kahdesta asiasta. Ensimmäinen on DAC (Digital-to-Analog Converter). Pidän sitä tärkeänä, koska esimerkiksi sen kautta teemme äänilähdön ESP32: ssa. Toinen ongelma, jota aiomme käsitellä tänään, on oskillaatio
