
Sisällysluettelo:
- Kirjoittaja John Day day@howwhatproduce.com.
- Public 2024-01-30 09:04.
- Viimeksi muokattu 2025-01-23 14:45.
Tämä opas kattaa joitakin matlabin perustoimintoja. Opit tekemään matlabista suorittamaan jaksollisen funktion sisäisesti ja piirtämään sen sekä piirtämään saman jaksollisen funktion Excel -tiedostosta ja piirtämään sen. Tämä ohje on tarkoitettu niille teistä, jotka eivät ole koskaan käyttäneet matlabia ja joiden on vain suoritettava yksinkertaisia tehtäviä sen kanssa. Kussakin kuvassa korostettu koodi sisältyy kommenttiin, joten voit kopioida ja liittää koodin. Voit vapaasti ottaa tämän koodin ja muokata sitä sovellukseesi sopivaksi.
Vaihe 1: Käynnistä Matlab
Ensimmäinen askel on saada matlab käyttöön ja aloittaa työskentely sen kanssa. Kun käynnistät matlabin ensimmäisen kerran, sen pitäisi näyttää alla olevasta kuvakaappauksesta. Ensimmäinen askel on määrittää hakemisto matlabille työskennellä. Ohjelma vetää sieltä kaikki tiedostot ja sinne kannattaa tallentaa kaikki matlab -työt. Suosittelen uuden kansion luomista jonnekin, jonka muistat, ja nimeämällä sen jotain, jonka tunnistat. Kun olet luonut uuden kansion, napsauta "…" näytön oikeassa yläkulmassa, kuten toisessa kuvassa on korostettu. Tämä tuo esiin selauslaatikon, kuten näkyy kolmannessa kuvassa. Etsi tietokoneellesi luomasi uusi kansio ja valitse se. Tässä esimerkissä tiedoston nimi on "370" ja se sijaitsee työpöydällä.
Vaihe 2: M-tiedoston luominen
Nyt meidän on tehtävä uusi M -tiedosto. M -tiedosto toimii aivan kuten koodin kirjoittaminen suoraan matlabiin, mutta voit tallentaa ja muokata koodia ja suorittaa sen toistuvasti. Kun syötät koodin suoraan matlabiin, kirjoita jokainen koodirivi erikseen. Kirjoita M -tiedostoon koko koodi ja suorita se kerralla. Avaa uusi M -tiedosto napsauttamalla tiedostoa. Vie kohdistin kohtaan "Uusi" ja napsauta sitten "Tyhjä M -tiedosto", kuten ensimmäisessä kuvassa. Koska tämä koodi voidaan suorittaa toistuvasti, on hyvä sulkea kaikki ja tyhjentää kaikki muuttujat ennen sen suorittamista joka kerta. Tämä tapahtuu kahdella koodirivillä: sulje kaikki selkeä kaikki Kuten kolmannesta kuvasta näkyy, varmistaa, että kaikki on tyhjennetty ja suljettu.
Vaihe 3: Aikavektorin luominen
Ensimmäinen asia, jonka teemme, on luoda graafi funktiosta matlabissa. Ensimmäinen askel on luoda riippumaton muuttuja. Tässä tapauksessa kutsumme sitä ajaksi "t". Menetelmä, jota käytämme tämän muuttujan luomisessa, on vektorin tekeminen. Vektori on pohjimmiltaan sarja numeroita. Esimerkiksi 1, 2, 3, 4 olisi lyhyt vektori. Koodi tämän vektorin luomiseksi on: t = 0,1: 0,01: 10; Ensimmäinen numero 0,1 viittaa alkupisteeseen. Toinen numero, 0.01, viittaa askelkoon. Kolmas numero 10 viittaa päätepisteeseen. Joten tämä vektori vastaa 0,1, 0,11, 0,12… aina 10 asti. Jos haluat nähdä, toimiiko vektorin luominen, napsauta toisessa kuvassa korostettua vihreää juoksupainiketta. Tämä suorittaa ohjelman. Jos haluat nähdä vektorin, siirry matlab -pääikkunaan. Napsauta työpöytää, vie hiiri työpöydän asettelun päälle ja napsauta sitten oletusarvoa kolmannen kuvan mukaisesti. Nyt näytön pitäisi näyttää neljänneltä kuvalta. Oikealla näet vasta luodun muuttujamme t. Kaksoisnapsauta sitä ja kuten viidennessä kuvassa näet luodun numerosarjan.
Vaihe 4: Toiminnon suorittaminen ja piirtäminen
Kaavataan nyt matlabissa luotu funktio. Ensimmäinen vaihe on luoda toiminto. Tämä on yhtä helppoa kuin halutun matemaattisen funktion kirjoittaminen. Esimerkki näkyy ensimmäisessä kuvassa. Tätä toimintoa varten käytetty koodi on: y = sin (t)+4*cos (5.*t).^2; Aika ennen kertomusta kosinissa ja ennen kosinin neliötä kehota matlabia suorittamaan nämä toiminnot yksinkertaisesti aikavektorin arvoesineille, älä käsittele aikavektoria matriisina ja yritä tehdä matriisitoimintoja sillä seuraava askel on luoda itse kuvio. Tämä tehdään käyttämällä toisessa kuvassa esitettyä koodia. Plot -komennon muuttujien järjestys on erittäin tärkeä, joten muista asettaa koodi aivan kuten alla. Figureh = axes ('fontsize', 14); plot (t, y, 'linewidth, 2) xlabel ('Aika (aika)') ylabel ('Y -arvo') Otsikko ('Y -arvo vs aika') ruudukko käytössä Lopuksi napsauta vain vihreää juoksunuolta uudelleen ja kuvan pitäisi ponnahtaa esiin kuten kolmannessa kuvassa.
Vaihe 5: Tietojen vetäminen Excelistä
Luomme nyt saman kaavion kuin aiemmin, mutta tuomalla funktiotiedot Excel -laskentataulukosta. Ensimmäinen kuva on kuvakaappaus käytettävästä Excel -laskentataulukosta. Se on täsmälleen samat datapisteet, jotka on luotu matlabissa aikaisemmissa vaiheissa, juuri tehty excelissä. Aloittaaksemme voimme poistaa aikavektorin luovan koodin ja toiminnon koodin edellisistä vaiheista. Koodisi pitäisi nyt näyttää toiselta kuvalta. Tämä on koodi Excel -tiedoston lukemiseen. "A" viittaa matriisiin, joka sisältää kaikki laskentataulukon numerot, ja "B" sisältää kaiken laskentataulukon tekstin. Muuttujat t ja y vedetään ensimmäisestä ja toisesta sarakkeesta koodin mukaisesti. [A, B] = xlsread ('excelexample.xlsx'); t = A (:, 1); y = A (:, 2); Kuvakoodia voidaan myös muuttaa kolmannen kuvan alemman punaisen laatikon mukaisesti. Tämä itse asiassa vetää kaavion otsikon ja akselitarrat laskentataulukosta ja laittaa ne kaavioosi. Xlabel (B (2)) ylabel (B (3)) Title (B (1)) Viimeinen tehtävä on suorittaa ohjelma uudelleen ja näet saman kuvan ponnahtavan esiin kuin lopullisessa kuvassa.
Vaihe 6: Specgramin luominen
Tässä vaiheessa käytämme matlabia luomaan specgram lukemalla wav -äänitiedosto. Spektogrammia kutsutaan joskus "2.5D -kuvaajaksi", koska se käyttää kaksiulotteista kuvaajaa, johon on lisätty väri amplitudin osoittamiseksi. Väri tarjoaa enemmän yksityiskohtia kuin yksinkertainen 2D -kuvaaja, mutta ei 3D -kuvaajan yksityiskohtia, joten termi "2.5D". Matlabin specgram -funktio ottaa joukon datapisteitä wav -tiedostosta ja suorittaa Fourier -muunnoksen pisteitä signaalin taajuuksien määrittämiseksi. Tämän ohjeen vuoksi ei ole tärkeää tietää, miten Fourier -muunnos toimii, vain tietää, että specgram piirtää läsnä olevat taajuudet ja kuinka vahvat ne ovat suhteessa aikaan. Toiminto piirtää ajan X-akselille ja taajuuden Y-akselille. Jokaisen taajuuden voimakkuus näkyy väreinä, tässä tapauksessa wav -tiedosto on äänitallenne iskukappaleesta ja sitten metallin värähtelyt tallennetaan äänenä. Spekgramin avulla voimme helposti määrittää metallikappaleen resonanssitaajuuden, koska se on taajuus, joka säilyy pisimpään ajan myötä. Tämän tehtävän suorittamiseksi sinun on ensin luettava matlab lukemaan wav -tiedosto käyttämällä seuraavaa koodia: [x, fs] = wavread ('flex4.wav'); Tässä tapauksessa flex4.wav on wav -tiedostomme otsikko, muuttuja x on tiedoston datapisteet ja fs viittaa näytteenottotaajuuteen., kirjoita vain seuraava koodi: specgram [x (:. 1), 256, fs]; 256 vastaa taajuutta, jolla FFT suoritetaan tietoja analysoitaessa. Matlab katkaisee pohjimmiltaan äänitiedoston paloiksi ja ottaa FFT: n kullekin palalle. 256 kertoo kuinka suuri kunkin palan pitäisi olla. Tämän yksityiskohdat eivät ole tärkeitä, ja 256 on turvallinen arvo käytettäväksi useimmissa sovelluksissa. Tästä on helppo nähdä, että resonanssitaajuus vastaa punaista huippua kuvan oikeassa alakulmassa. Tämä on huippu, joka kestää pisimpään ajan suhteen.
Suositeltava:
Juotospinta -asennuskomponentit - Juottamisen perusteet: 9 vaihetta (kuvilla)

Juotospinta -asennuskomponentit | Juotosmenetelmän perusteet: Tähän asti juottamisen perusteet -sarjassa olen keskustellut riittävästi juottamisen perusteista, jotta voit aloittaa harjoittelun. Tässä opetusohjelmassa keskustelen hieman kehittyneemmästä, mutta se on joitakin Surface Mount Compon juottamisen perusasioita
Raspberry Pi: n hallinta Matlabin avulla: 5 vaihetta

Raspberry Pi: n hallinta Matlabin avulla: Hei, tämä opetusohjelma käsittelee päätön vadelmapii: n hallintaa matlabin avulla. Saatat joutua asentamaan matlabin uusimpaan versioon, jos haluat tukea uudemmalle vadelmapi -levylle
Aikuisten kuulotestin tekeminen MATLABin avulla: 6 vaihetta

Aikuisten kuulotestin tekeminen MATLABin avulla: VASTUUVAPAUSLAUSEKE: Testimme EI ole lääketieteellinen diagnoosi, eikä sitä tule käyttää sellaisenaan. Jos haluat mitata kuulosi tarkasti, ota yhteyttä lääkäriin. Käyttämällä jo olemassa olevia materiaaleja ryhmämme teki kuulotestin. Testi on tarkoitettu vain aikuisille ja nuorille
Aivokasvaimen magneettikuvaus Matlabin avulla: 6 vaihetta
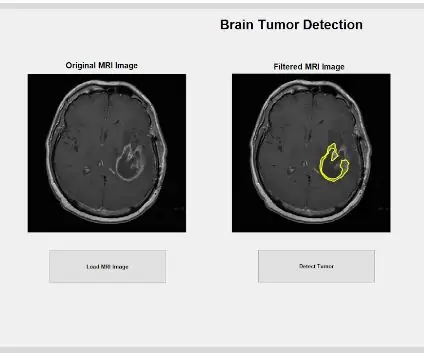
Aivokasvaimen magneettikuvaus Matlabin avulla: Kirjoittaja: Madhumita Kannan, Henry Nguyen, Ashley Urrutia Avila, Mei JinTämä MATLAB -koodi on ohjelma, joka tunnistaa potilaan aivojen magneettikuvauksessa löydetyn kasvaimen tarkan koon, muodon ja sijainnin. Tämä ohjelma on suunniteltu toimimaan alun perin kasvainten havaitsemisen kanssa
Diabeettisen retinopatian automaattinen diagnoosi MATLABin kautta: 33 vaihetta
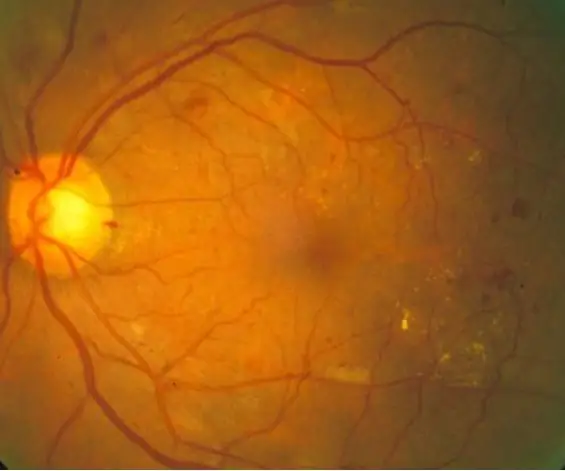
Diabeettisen retinopatian automaattinen diagnoosi MATLABin kautta: (Katso yllä oleva koodi) Diabeettinen retinopatia on diabetekseen liittyvä silmäsairaus, jonka aiheuttaa korkea verensokeri. Korkea verensokeritaso saa verkkokalvon verisuonet turpoamaan, mikä johtaa verisuonten laajentumiseen ja jopa
