Totuustaulukoiden ratkaiseminen: 10 vaihetta

2024 Kirjoittaja: John Day | [email protected]. Viimeksi muokattu: 2024-01-30 09:00

Totuustaulukko on tapa visualisoida kaikki ongelman tulokset. Tämä ohjesarja on tarkoitettu ihmisille, jotka aloittavat diskreetin matematiikan. Harjoittelemme tänään esimerkkiongelmaa, joka liittyy näihin ohjeisiin. Tarvitset raaputuspaperin ja lyijykynän pöydän visualisoimiseksi. Tämän ongelman pitäisi kestää noin 5 minuuttia, jos ihmiset tietävät aiheesta etukäteen ja noin 10 minuuttia aloittelijoille.

Tässä ohjeessa keskitymme ongelmaan ~ p Λ q. Käytämme tätä esitelläksemme joitain symboleja, joita tarvitaan totuustaulukoiden tulkitsemiseen.

Vaihe 1: Totuustaulukoiden ymmärtäminen

Totuustaulukko on tapa visualisoida ongelman kaikki mahdollisuudet. Totuustaulukoiden tunteminen on erillinen matematiikan perusedellytys. Täältä löydät kaikki tulokset yksinkertaiselle yhtälölle ~ p Λ q.

Vaihe 2: Symbolien tunteminen

Ensimmäinen askel totuuspöydälle on merkkien ymmärtäminen. "~" Tässä ongelmassa tarkoittaa kieltämistä. P ja q ovat molemmat muuttujia. "Λ" vastaa "ja". Tämä yhtälö luetaan "ei p ja q", eli yhtälö on totta, jos p ei ole totta ja q on totta.

Vaihe 3: Taulukon muotoilu

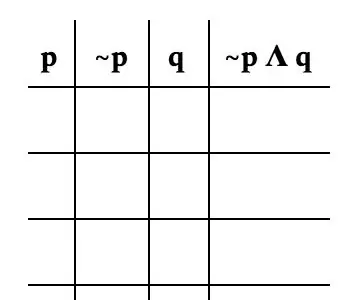
Muodosta nyt todellinen taulukko. On tärkeää jakaa ongelma jokaisen muuttujan mukaan. Tätä ongelmaa varten jaamme sen seuraavasti: p, ~ p, q ja ~ p Λ q. Kuva on hyvä esimerkki siitä, miltä pöytäsi näyttää.

Vaihe 4: Tosi ja epätosi määrittäminen

Koska muuttujia on vain kaksi, muuttujia on vain neljä. P: n osalta jaamme sen puoleen välilyönneistä, jotka on otettu T: llä (tosi) ja toinen puoli F: llä (väärille).

Vaihe 5: Kieltäminen

Kirjoita ~ p: lle päinvastainen merkki, joka p: llä on, koska ~ p on p: n vastakohta.

Vaihe 6: Muuttuja "q"

Jos käytät q: tä, vaihdat T: n ja F: n välillä saadaksesi mahdollisen yhdistelmän. Koska yhtälö keskittyy vain ~ p: hen, voimme jättää p -sarakkeen huomiotta määritettäessä yhtälön totuutta. "Λ" -symboli tarkoittaa, että sekä ~ p: n että q: n on oltava totta, jotta yhtälö olisi totta.

Vaihe 7: Väärän ratkaiseminen viimeisessä sarakkeessa

Ensimmäisellä rivillä, koska ~ p on F ja q on T, ~ p Λ q on F skenaariossa, jossa ~ p on F ja q on T. Ainoa skenaario, jossa yhtälö on T, jossa ~ p on T ja q on T.

Vaihe 8: Totuuden löytäminen viimeisestä sarakkeesta

Tämä tarkoittaa, että ainoa T -rivi on kolmas.

Vaihe 9: Taulukon viimeistely

Tarkista, että taulukko on oikein. Voit tehdä tämän tarkistamalla, että merkit ovat oikein ja varmista, että viimeinen sarake on tehty oikein. Viimeinen sarake on kaikkien muuttujien mahdollisten muutosten tulos.

Vaihe 10: Valmis

Nyt kun tiedät, miten perustotuuden taulukko tehdään, jatka harjoittelua! Mitä enemmän harjoittelet, sitä paremmin pääset tekemään niitä.