Perus 3D -skanneri digitaaliseen 3D -kartoitukseen: 5 vaihetta

2024 Kirjoittaja: John Day | [email protected]. Viimeksi muokattu: 2024-01-30 09:00

Tässä projektissa kuvailen ja selitän 3D-skannauksen ja rekonstruktion perusperiaatteet, joita sovelletaan pääasiassa pienten puolitasoisten esineiden skannaukseen ja joiden toimintaa voidaan laajentaa koskemaan skannaus- ja jälleenrakennusjärjestelmiä, jotka voidaan asentaa kauko-ohjattaviin lentokoneisiin 3D -malli. paikoista, joihin niitä kuljettava lentokone lentää

Lopullinen ajatus on saada 3D -skannaus jostakin paikasta tai alueesta, joko sen ulko- tai sisäpuolelta, ja käyttää sitä digitaalisena karttana (kuten Prometeuksen elokuvassa)

Vaihe 1:

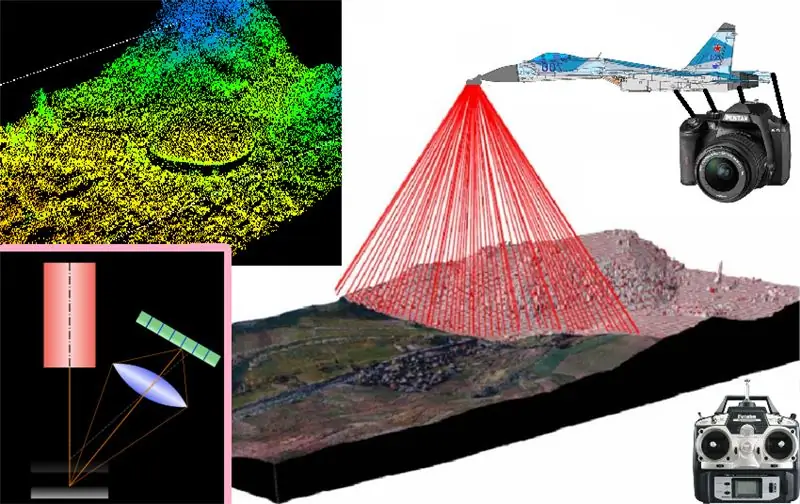
ajatuksena on asentaa koko 3D-skannausjärjestelmä kauko-ohjattavalle tasolle, jotta voidaan digitalisoida minkä tahansa alueen virtuaalinen kartta, jonka yli se lentää kolmiulotteisena, mutta tätä varten aloitimme laserkolmiomittauksen toiminnan alusta skannaus tai kolmiulotteinen rekonstruktio laserkolmioinnilla koostuu pohjimmiltaan lasersäteen kuljettamisesta prisman läpi, joka muodostaa laserraidan, jotta saadaan koko laserraita, joka heijastetaan skannattavaan kohteeseen, ja kun tämä laserprojektio on saavutettu pintapinta Skannauspaikasta kuva on otettava tietyntyyppisellä kameralla ja mieluiten tietäen kulma, joka muodostuu suhteessa lähetetyn laserraidan heijastuskulmaan, koska jokainen näistä kuvista kaappaa heijastetut lasernauhat. Objektin pinnalla ne esikäsitellään skannattavan kohteen mittaominaisuuksien poimimiseksi ja skannataan yksinkertaisesti nauhalta nauhalla kohteen yläpuolelle, jotta saadaan sen pinnan profiili kyseisen kohteen poikittaisessa segmentissä, ja sitten kaapata kohteen seuraavan poikkileikkauksen projisoidun nauhan, jotta kaikki projisoidut raidat lisätään yhteen Ennen kaikkia obton poikkileikkauksia saamme sen pinnan kolmiulotteisen skannauksen

Vaihe 2:

Koska olemme tunnistaneet tavoitteemme, seuraava askel tietäen, että nousemiseksi sinun on ensin pidettävä jalat tukevasti maassa, joten aloitimme kentällä lineaarisen 3D -skannerin kokeellisella prototyypillä varmistaaksemme peruslaitteen oikean toiminnan. 3D -skannaus ja kuten yllä olevasta kuvasta näkyy, käytin tietokonetta, OpenCV: tä, OpenGL: n liimaa, verkkokameraa, laser-, laser -maatilageneraattoria (tässä tapauksessa pyörivän peilin kautta), elektronista lineaarista siirtymäjärjestelmää (tehty kiskolla) ja järjestelmä, joka on uutettu vanhasta tulostimesta) alustalta, jolle asetan skannattavat kohteet, puun ja muovailupohjan, ja kuten kuvasta näkyy, tietokoneella: onnistuin luomaan ja näyttämään Gluteen OpenGL: stä kolme- ulottuvuusmalli, joka on toistettu skannatun todellisen kohteen (tässä tapauksessa leluhämähäkki) perusteella

joten on enemmän kuin ilmeistä, että toimintaperiaate on toimiva ja että sen mukautuksilla ja mukautuksilla lentävään järjestelmään se voi skannata ja toistaa 3D -kartan alueesta, jolla se lentää.

Mutta tämä järjestelmä palvelee vain 3D -karttojen hankkimista paikoista, joiden yli se lentää ???…

Vaihe 3:

luolien ja kanavien sisätilan kartoitus (aivan kuten Prometeus-elokuvassa) Tämä 3D-skannausjärjestelmä toimii myös rekonstruoimaan kolmiulotteisia malleja suurten ja onttojen esineiden, kuten luolien, rakennusten, tunneleiden jne. sisätiloista. sen toimintaperiaate on täsmälleen sama kuin jo kuvattu ja joka koostuu pohjimmiltaan seuraavista:

1. ottaa valokuvan jokaisesta laserraidan projektiosta skannattavalle pinnalle
2. suodattaa ja poistaa värit kuvasta
3. binaarista väri dynaamisella kuvakynnyksellä
4. käytä reunatunnistinta tunnistamaan kunkin laserprojektion poikkileikkauksen kaapattu profiili
5. ja valitse segmentoinnin avulla sopiva reuna skannattavan ja rekonstruoitavan objektin poikkileikkauksen kolmiulotteiselle esitykselle virtuaalisessa 3D -kartassa
6. sitten nämä vaiheet toistetaan yksinkertaisesti jokaiselle valokuvalle, joka on otettu osa-alueella laserraidoista, jotka heijastavat jatkuvasti kunkin alajakson alaosa.

kerros kerroksittain poikkileikkausten esityksiä lisätään peräkkäin, kunnes saadaan pistepilvi, joka muodostuu monista kartoitettavan kohteen poikkileikkausten esityksistä

Vaihe 4:

Sitten läpäisen pinnallisten lasernauhojen projektioiden kuvankäsittelyohjelmat. ja näiden sussive poikittaisten esitysten virtuaalinen 3D-rekonstruktio kehitetyssä kolmiulotteisessa karttamallissa:

kuvankäsittely:

n

#include #include "cv.h" #include "highgui.h" #include // #include #include #include #include

char f = 0; char -nimi = {"0.jpg"}; int n = 0, s, x, y; CvScalar sp; TIEDOSTO *NuPu;

void Writepoints () {char bufferx [33], puskurointi [33]; itoa (x, puskuri, 10); itoa (y, puskurointi, 10); fprintf (NuPu, puskuri); fprintf (NuPu, "\ t"); fprintf (NuPu, puskurointi); fprintf (NuPu, "\ n"); }

void noteblockInit () {NuPu = fopen ("NuPu.txt", "w"); fseek (NuPu, 0, 0); fprintf (NuPu, "NP:"); fprintf (NuPu, "\ n"); }

int main () {char argstr [128]; noteblockInit (); cout << "Teklea!…:" f; nimi [0] = f; cout <

IplImage* img0 = cvLoadImage ("00.jpg", 0); jos (f == '0') {for (y = 1; yheight-2; y ++) {for (x = 1; xwidth-2; x ++) {sp = cvGet2D (img0, y, x); jos (sp.val [0]> 50) {Writepoints (); n ++;}}}} else {for (y = 1; yheight-2; y ++) {for (x = 1; xwidth-2; x ++) { sp = cvGet2D (img1, y, x); if (sp.val [0]> 50) {Writepoints (); n ++;}}}} char puskuri [33]; itoa (n, puskuri, 10); fprintf (NuPu, "Fin:"); fprintf (NuPu, puskuri); fprintf (NuPu, "\ n"); fclose (NuPu);

cvWaitKey (0); //_execlp("calc.exe "," calc.exe ", argstr, NULL); cvDestroyAllWindows (); cvReleaseImage (& kuva); cvReleaseImage (& img); cvReleaseImage (& img0); cvReleaseImage (& img1); cvReleaseImage (& img2); palauta 0; }

3D -rekonstruktio:

#include //////////////////ififf _APPLE_ #include #else #include #include #endif #include #include #include #include #include #include

#define violeta glColor3f (1, 0, 1) #define azul glColor3f (0, 0, 1) #define turkeza glColor3f (0, 1, 1) #define verde glColor3f (0, 1, 0) #define amarillo glColor3f (1, 1, 0) #define naranja glColor3f (1,.3, 0) #define rojo glColor3f (1, 0, 0) käyttämällä nimiavaruutta std; int s, Boton = 1, Pulbut = 1; float mx = 0, my = 0, mtx = 0, mty = 0, mtz = -5,0; const int Avance = 1; merkkijono, Aux; char Merkki = 'H'; TIEDOSTO *NuPu; int NP, h, w; float G = 0, n = 0, cx [5000], cy [5000], x, y, ax, ay, az; int fontti = (int) GLUT_BITMAP_8_BY_13; staattisen hiilen tarra [100]; hiilipuskuri [3]; GLfloat anguloCuboX = 0.0f; GLfloat anguloCuboY = 0.0f; GLfloat anguloEsfera = 0,0f; GLint ancho = 500; GLint alto = 500; int hazPerspectiva = 0; void reshape (int leveys, int korkeus) {glViewport (0, 0, leveys, korkeus); glMatrixMode (GL_PROJECTION); glLoadIdentity (); jos (hazPerspectiva) gluPerspective (23.0f, (GLfloat) leveys/(GLfloat) korkeus, 1.0f, 20.0f); muut glOrtho (-1, 1, -1, 1, -10, 10); glMatrixMode (GL_MODELVIEW); ancho = leveys; alto = korkeus; } mitätön Kolorear (int K) {float Hip; x = (cx [s] -320)/480; y = (cy [s] -240)/640; Lantio = neliömetriä (pow (x, 2)+pow (y, 2)); jos ((Hip> = 0) && (Hip =.07) && (Hip =.14) && (Hip =.21) && (Hip =.28) && (Hip =.35) && (Hip =.42) && (Hip <=. 49)) {violeta;}} void drawNuPu (void) {glColor3f (1, 1, 1); glBegin (GL_LINES); glVertex3f (.2, 0, 0); glVertex3f (-.2, 0, 0); glVertex3f (0,.2, 0); glVertex3f (0, -2, 0); glEnd (); rojo; glBegin (GL_POINTS); for (n = 0; n <10; n ++) {for (s = 0; s void setOrthographicProjection () {glMatrixMode (GL_PROJECTION); glPushMatrix (); glLoadIdentity (); gluOrtho2D (0, w, 0, h); glScalef (1, -1, 1); glTranslatef (0, -h, 0); glMatrixMode (GL_MODELVIEW);} void renderBitmapString (float x, float y, void *font, char *string) {char *c; glRasterPos2f (x, y); for (c = string; *c! = '\ 0'; c ++) {glutBitmapCharacter (font, *c);}} void display () {// mx = 468; itoa (mx, puskuri, 10); glClear (GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // glLoadIdentity (); glColor3f (1.0, 1.0, 1.0); glRasterPos2f (-1,.9); // glutBitmapString (GLUT_BITMAP_TIMES;; s <3; s ++) {glutBitmapCharacter (GLUT_BITMAP_TIMES_ROMAN_24, puskuri [s]);} glTranslatef (mty, -mtx, mtz); glRotatef (mx, 1.0f, 0.0f, 0.0f); glRotatef (my, 0.0f, 1.0f, 0.0f); drawNuPu (); /*glColor3f(1.0, 1.0, 1.0); glRasterPos2f (.5,.5); // glutBitmapString (GLUT_BITMAP_TIMES_ROMAN_24, "Hello Text"); glutBitmapCharacterAP (GLU_BIM_));* / /*glColor3f (1. 0f, 1,0f, 1,0f); setOrthographicProjection (); glPushMatrix (); glLoadIdentity (); renderBitmapString (30, 15, (void *) fontti, "GLUT Tutorial ---_ ------ _@ 3D Tech"); */ glFlush (); glutSwapBuffers (); anguloCuboX+= 0,1f; anguloCuboY+= 0,1f; anguloEsfera+= 0,2f; } void init () {glClearColor (0, 0, 0, 0); glEnable (GL_DEPTH_TEST); ankkuri = 500; alto = 500; } void leer () {ifstream myfile ("A:/Respaldo syyskuu 2016/D/Respaldos/Respaldo compu CICATA abril 2015/usb1/rekostruccion 3D fi Especialidad CICATA/Software/Reconstruccion 3D/R3d_0 / bin/Debug/NuPu.txt"); jos (myfile.is_open ()) {s = 0; while (getline (oma tiedosto, rivi)) {if ((rivi [0]! = 'N') && (rivi [0]! = 'F')) {Aux = rivi; rivi [0] = 48; rivi [1] = 48; linja [2] = 48; rivi [3] = 48; cy [s] = atoi (line.c_str ()); Aux [4] = 48; Aux [5] = 48; Aux [6] = 48; // Aux [7] = 48; cx [s] = atoi (Aux.c_str ()); s ++; }} myfile.close (); } else cout <1780) NP = 1700; cout <void idle () {display (); } tyhjä näppäimistö (allekirjoittamaton char -näppäin, int x, int y) {kytkin (näppäin) {case 'p': case 'P': hazPerspectiva = 1; uudistaa (ancho, alto); tauko; tapaus 'o': tapaus 'O': hazPerspectiva = 0; uudistaa (ancho, alto); tauko; tapaus 27: // paeta poistuminen (0); tauko; }} void raton (int -painike, int -tila, int x, int y) { / * GLUT_LEFT_BUTTON 0 GLUT_MIDDLE_BUTTON 1 GLUT_RIGHT_BUTTON 2 GLUT_DOWN 0 GLUT_UP 1 * / Boton = -painike; Pulbut = tila; // mx = y; näyttö(); } void ratmov (int x, int y) {if ((Boton == 0) & (Pulbut == 0)) {mx = y; minun = x; } jos ((Boton == 2) & (Pulbut == 0)) {mtx = (y/200) -1; mty = (x/200) -1; } jos ((Boton == 1) & (Pulbut == 0)) {mtz =-(y/40) -5; } näyttö (); } int main (int argc, char ** argv) { /*glutAddMenuEntry () glutAddSubMenu () glutAttachMenu () glutCreateMenu () glutSetMenu () glutStrokeCharacter () glutStrokeLength ()* / /*gl Lue pikselien lukeminen () kehyspuskuri glGetPixelMapfv () palauttaa määritetyn pikselikartan glGetPixelMapuiv () palauttaa määritetyn pikselikartan glGetPointerv () Palauttaa määritetyn osoittimen osoitteen.*/ Init (); leer (); glutInit (& argc, argv); glutInitDisplayMode (GLUT_DOUBLE | GLUT_RGB); glutInitWindowPosition (50, 50); glutInitWindowSize (ancho, alto); glutCreateWindow ("Cubo 1"); sen sisällä(); glutDisplayFunc (näyttö); glutReshapeFunc (muotoile); glutIdleFunc (joutokäynti); glutMouseFunc (raton); glutMotionFunc (ratmov); glutKeyboardFunc (näppäimistö); glutMainLoop (); palauta 0; }

Vaihe 5:

hetkeksi minun on lopetettava! … Mutta seuraavassa luvussa lupaan teille, että käytän sitä vadelmapi 3: lläni tai jetson-nanopöydälläni, joka on jo asennettu joihinkin kauko-ohjattaviin lentokoneisiin, tai johonkin hämähäkkirobottiin luolien sisätilan skannaamiseksi