Matriisin rekursiivinen yhteenveto Javassa: 9 vaihetta

2025 Kirjoittaja: John Day | [email protected]. Viimeksi muokattu: 2025-01-23 14:41

Rekursio on erittäin hyödyllinen ja aikaa säästävä menettely, joka voi nopeasti ratkaista ongelman hyvin pienellä koodilla. Rekursio sisältää itse luomasi menetelmän, joka lyhentää alkuperäistä ongelmaa.

Tässä esimerkissä laskemme yhteen kymmenen kokonaisluvun taulukon, mutta koko voi olla minkä tahansa pituinen.

Tarvikkeet

Sinun pitäisi tuntea javan perussyntaksi ja saada IDE tai tekstieditori kirjoittaaksesi koodisi tähän tehtävään.

Vaihe 1: Määritä päämenetelmäsi

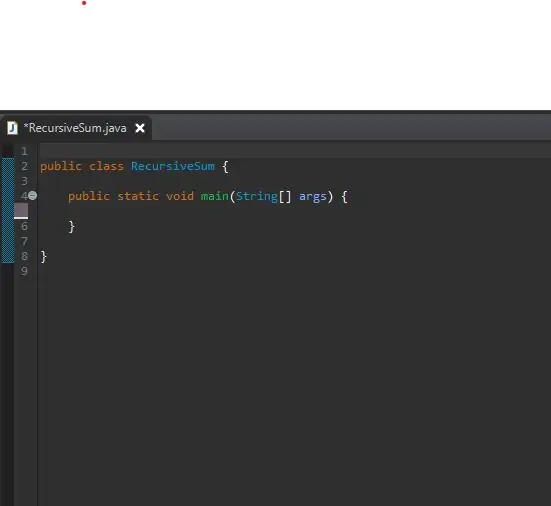
Aloita asettamalla päämenetelmäsi juuri luodulle luokalle. Olen antanut luokalleni nimen RecursiveSum. Tässä voit luoda kokonaislukuryhmän ja kutsua rekursiivisen menetelmän.

Vaihe 2: Luo rekursiivinen menetelmäotsikko

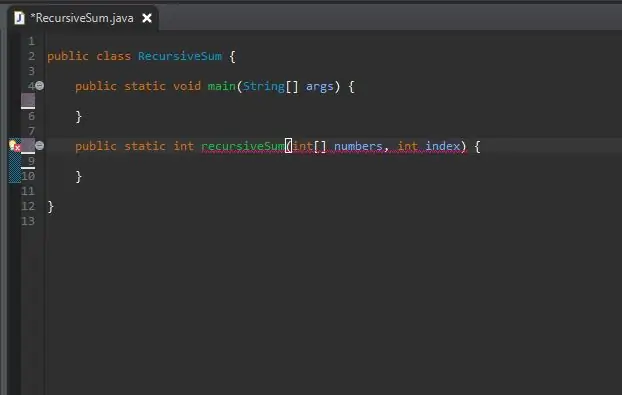
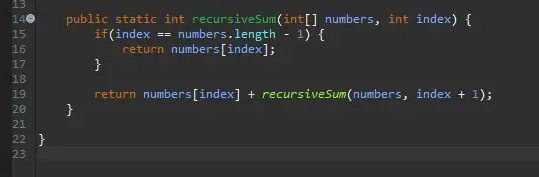
Luo päämenetelmän ulkopuolella rekursiiviselle menetelmällesi menetelmäotsikko.

Menetelmä on staattinen, koska se ei vaadi objektia sen käyttämiseen.

Palautustyyppi on int, koska käyttämämme taulukko on täynnä kokonaislukuja. Tämä voidaan kuitenkin muuttaa mihin tahansa numerotyyppiin, jota taulukko sisältää.

Olen antanut menetelmälleni recursiveSum, joka ottaa kaksi parametria; joukko kokonaislukuja ja indeksi, jonka lisäämme summaan. Olen kutsunut nämä parametrit numeroiksi ja indeksiksi.

Näet virheitä heti ja se on hyvä. Ne korjataan myöhemmin.

Vaihe 3: Luo Kicker/base Case

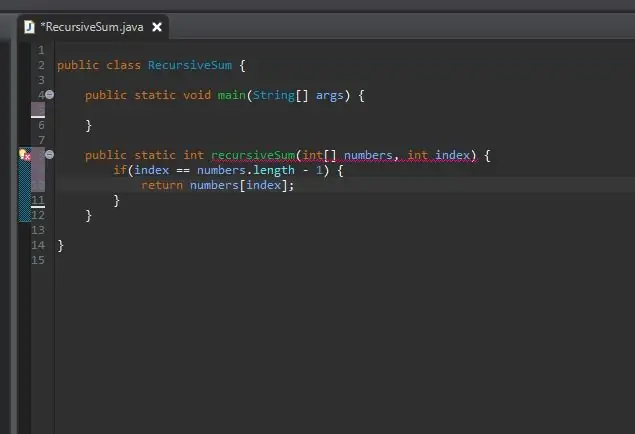
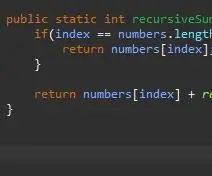
Rekursiivinen menetelmä tarvitsee potkurin/perustapauksen. Tämä on tila, joka estää menetelmääsi loputtomasti kutsumasta itseään. Tätä perustapausta voidaan pitää yksinkertaisimpana tapauksena, jonka kohtaamme. Tässä tapauksessa perustapaus on silloin, kun olemme ryhmämme lopussa. Jos nykyinen indeksi on yhtä suuri kuin taulukon pituus (miinus 1, koska taulukot alkavat laskea 0: sta 1: een), olemme lopussa ja palautamme kyseisen elementin kyseiselle indeksille.

Vaihe 4: Rekursiivinen vaihe

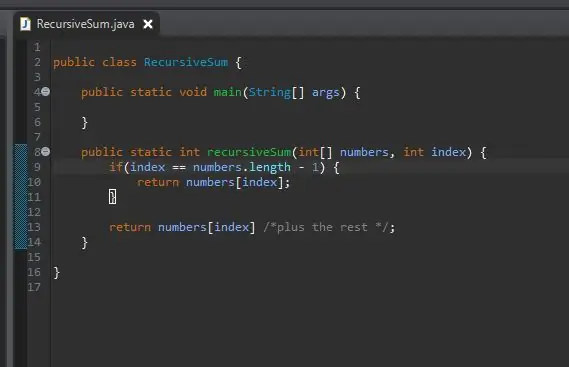
Kun meillä on perustapaus, seuraava askel on rekursiivinen vaiheemme. Tässä tapahtuu taikuutta. Olemme käsitelleet tapauksen, jossa indeksimme on taulukon viimeinen elementti. Entä jos emme ole ryhmämme viimeisessä elementissä? Entä jos voisimme yksinkertaisesti pyytää sitä lisäämään nykyisen elementtimme ja seuraavan? Lopulta saavutamme joukkomme loppuun ja peruskotelomme vaikuttaa.

Tämän saavuttamiseksi palaamme yksinkertaisesti nykyisen hakemistomme ja "lisäämme loput" taulukosta.

Vaihe 5: Lyhennä ongelmaa

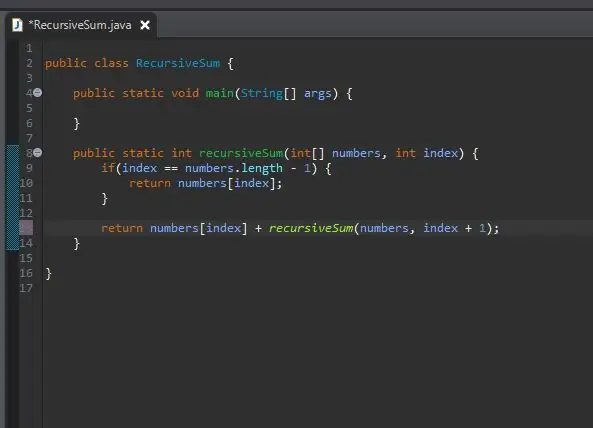
Miten yksinkertaisesti "lisätään loput"? Meillä on jo menetelmä, joka lisää tietyn elementin; meidän rekursiivinenSum () -menetelmämme! Voimme kutsua sitä uudelleen, mutta muuta, mitä indeksiä laskemme yhteen.

Välitämme samassa taulukossa, jota käsittelemme, mutta välitämme seuraavan indeksin nykyisestä indeksistämme. Teemme tämän yksinkertaisesti lisäämällä yhden nykyiseen hakemistoomme kuvan mukaisesti.

Vaihe 6: Luo kokonaislukujärjestelmä

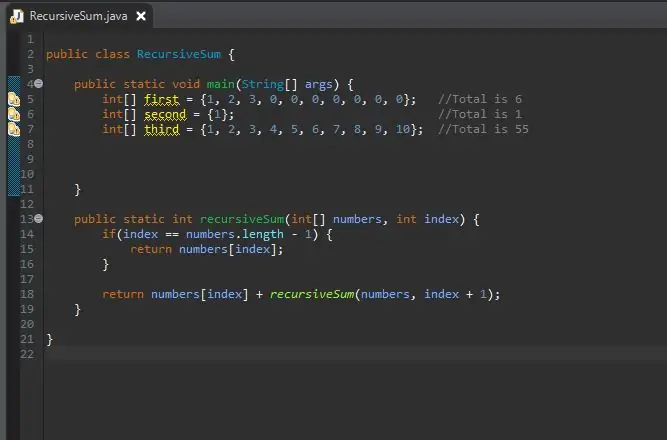
Nyt kun rekursiivinen summausmenetelmämme on valmis, voimme luoda taulukon, jota käsittelemme. Tämä taulukko on päämenetelmälohkossamme.

Voit tehdä taulukon koosta niin kauan kuin haluat. Olen luonut muutamia eri kokoja ja arvoja sisältäviä matriiseja osoittaakseni, että se ei toimi vain yhden koon kanssa.

Vaihe 7: Kutsu menetelmä joukkoosi

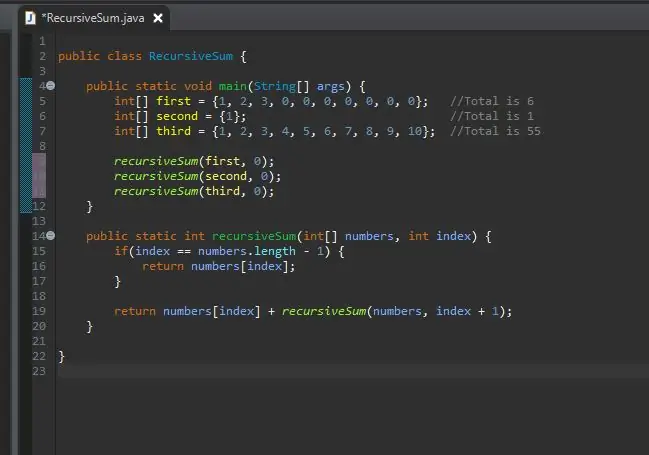
Nyt voit kutsua rekursiivisen menetelmän ja siirtää nämä taulukot sille. Nyt voit suorittaa ohjelman.

Vaihe 8: Tulosta tulokset

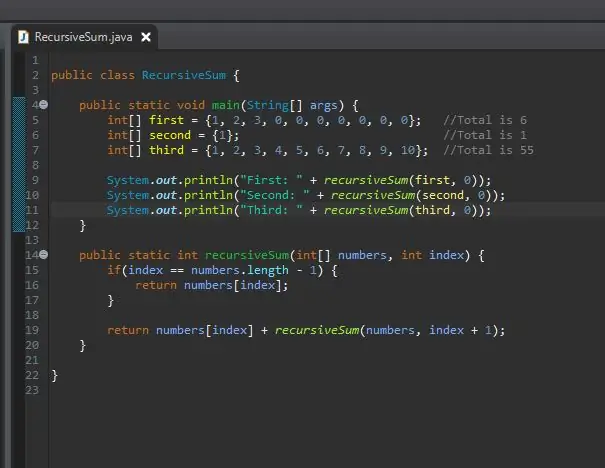
Mitään ei tapahtunut. Miksi? Rekursiivinen summa palauttaa kokonaisluvun, mutta emme ole tehneet mitään tälle kokonaisluvulle. Se teki tehtävänsä, mutta emme näe tulosta. Tuloksen saamiseksi tulostamme sen vain niin. Tämän suorittamisen jälkeen sinun pitäisi nähdä kunkin taulukon tulokset.

Vaihe 9: Onnittelut

Olet suorittanut rekursiivisen toiminnon. Voit vapaasti muuttaa matriisisi kokoa. Jos testaat sitä, huomaat sen kaatuvan, kun sinulla on tyhjä taulukko. Emme ole ottaneet sitä huomioon, mutta se on loistava tapa parantaa rekursiivista menetelmääsi.