Itsetasapainottava robotti käyttäen PID -algoritmia (STM MC): 9 vaihetta

2024 Kirjoittaja: John Day | [email protected]. Viimeksi muokattu: 2024-01-30 09:03

Viime aikoina on tehty paljon töitä esineiden itsetasapainottamisessa. Itsetasapainon käsite alkoi käänteisen heilurin tasapainottamisesta. Tämä käsite ulottui myös lentokoneiden suunnitteluun. Tässä projektissa olemme suunnitelleet pienen itsetasapainottavan robotin mallin käyttämällä PID (Proportional, Integral, Derivative) -algoritmia. Siitä lähtien tämä menetelmä on teollisten prosessinohjausjärjestelmien uusi kasvot. Tässä raportissa tarkastellaan esineiden itsetasapainottamiseen liittyviä menetelmiä. Tämä projekti toteutettiin lukukauden projektina ymmärtääkseen PID: n korrelaation eri teollisuusprosessien tehokkuuteen. Tässä keskitytään vain lyhyen katsauksen antamiseen PID -valvonnan tehokkuudesta ja soveltamisesta. Tämä asiakirja on kehitetty tarjoamalla lyhyt johdatus ohjausjärjestelmiin ja niihin liittyviin terminologioihin sekä hankkeen motiiveja. Kokeita ja havaintoja on tehty, ansioita ja haittoja on kuvattu päättymällä tuleviin parannuksiin. Itsetasapainottavan robotin malli kehitettiin ymmärtämään PID: n tehokkuus ohjausjärjestelmän maailmassa. Joidenkin tiukkojen testien ja kokeiden kautta havaittiin PID -ohjausjärjestelmän edut ja haitat. Todettiin, että huolimatta monista PID -ohjauksen eduista aiempiin menetelmiin verrattuna, tämä järjestelmä vaatii silti paljon parannuksia. Toivotaan, että lukija ymmärtää hyvin itsetasapainon tärkeyden, PID -valvonnan tehokkuuden ja puutteet

Vaihe 1: Johdanto

Tietokoneiden ja prosessien teollistumisen myötä koko ihmiskunnan historian ajan on aina tehty tutkimusta, jolla kehitetään tapoja kehittää prosesseja ja mikä tärkeintä, hallita niitä itsenäisesti koneilla. Tavoitteena on vähentää ihmisten osallistumista näihin prosesseihin ja siten vähentää virheitä näissä prosesseissa. Siksi kehitettiin”ohjausjärjestelmätekniikan” ala. Ohjausjärjestelmätekniikka voidaan määritellä käyttämällä eri menetelmiä prosessin toiminnan ohjaamiseen tai jatkuvan ja edullisen ympäristön ylläpitoon, olipa se sitten manuaalinen tai automaattinen.

Yksinkertainen esimerkki voisi olla huoneen lämpötilan säätäminen. Manuaalinen ohjaus tarkoittaa henkilön läsnäoloa paikassa, joka tarkistaa nykyiset olosuhteet (anturi), vertaa sitä haluttuun arvoon (käsittely) ja ryhtyy tarvittaviin toimiin halutun arvon saamiseksi (toimilaite). Tämän menetelmän ongelma on se, että se ei ole kovin luotettava, koska henkilö on altis virheilleen tai huolimattomuudelleen työssään. Toinen ongelma on myös se, että toimilaitteen käynnistämän prosessin nopeus ei ole aina tasainen, eli joskus se voi tapahtua vaadittua nopeammin tai joskus hitaasti. Ratkaisu tähän ongelmaan oli käyttää mikro-ohjainta järjestelmän ohjaamiseen. Mikro-ohjain on

ohjelmoitu ohjaamaan prosessia annettujen spesifikaatioiden mukaisesti, kytketty piiriin (keskustellaan myöhemmin), syötetty haluttuun arvoon tai olosuhteisiin ja ohjaa siten prosessia halutun arvon ylläpitämiseksi. Tämän prosessin etuna on se, että ihmisen ei tarvitse puuttua tähän prosessiin. Myös prosessin nopeus on yhtenäinen

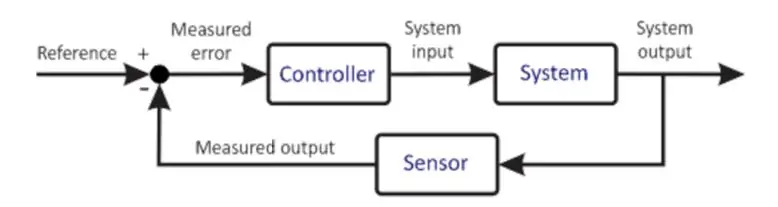
Perusohjausjärjestelmä

Edellinen kaavio esittää hyvin yksinkertaistetun version ohjausjärjestelmästä. Mikro -ohjain on minkä tahansa ohjausjärjestelmän ydin. Se on erittäin tärkeä komponentti, joten sen valinta tulee tehdä huolellisesti järjestelmän vaatimusten perusteella. Mikro-ohjain vastaanottaa syötteen käyttäjältä. Tämä tulo määrittää järjestelmän halutun tilan. Mikro-ohjain saa myös anturin antaman takaisinkytkennän. Tämä anturi on kytketty järjestelmän lähtöön, jonka tiedot syötetään takaisin tuloon. Ohjelmointiin perustuva mikroprosessori suorittaa erilaisia laskelmia ja antaa ulostulon toimilaitteelle. Toimilaite ohjaa tehoon perustuen laitosta yrittääkseen ylläpitää näitä olosuhteita. Esimerkki voisi olla moottoriajuri, joka ajaa moottoria, jossa moottori on toimilaite ja moottori on laitos. Moottori pyörii siten tietyllä nopeudella. Liitetty anturi lukee laitoksen nykyisen tilan ja syöttää sen takaisin mikro-ohjaimeen. Mikro-ohjain vertaa jälleen, tekee laskelmia ja siten sykli toistaa itseään. Tämä prosessi on toistuva ja loputon, jolloin mikro-ohjain ylläpitää halutut olosuhteet

Vaihe 2: PID -pohjainen ohjausjärjestelmä

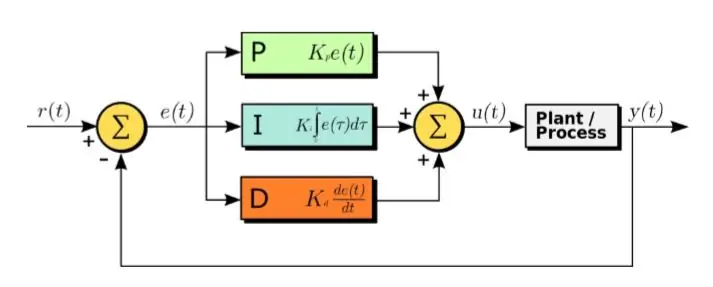
PID -algoritmi on tehokas menetelmä ohjausjärjestelmän suunnitteluun.

Määritelmä

PID tarkoittaa suhteellista, integroitua ja johdannaista. Tässä algoritmissa vastaanotettu virhesignaali on tulo. Virhesignaaliin sovelletaan seuraavaa yhtälöä

U (t) = Kp ∗ e (t) + Kd ∗ d/dt (e (t)) + Ki ∗ integraali (e (t)) (1.1)

Lyhyt selitys

Kuten yllä olevasta yhtälöstä voidaan nähdä, virhesignaalien integraali ja derivaatta lasketaan, kerrotaan niiden vakioilla ja lisätään yhdessä vakion Kp kanssa kerrottuna e (t): llä. Lähtö syötetään sitten toimilaitteeseen, joka saa järjestelmän toimimaan. Katsotaan nyt vuorotellen kunkin toiminnon osaa. Tämä toiminto vaikuttaa suoraan nousuaikaan, laskuaikaan, huippuhetkeen, asettumisaikaan ja vakaan tilan virheeseen.

• Suhteellinen osa: Suhteellinen osa lyhentää nousuaikaa ja pienentää vakaan tilan virhettä. Tämä tarkoittaa sitä, että järjestelmä saavuttaa huippuarvonsa vähemmän aikaa ja kun se saavuttaa vakaan tilansa, vakaan tilan virhe on pieni. Se kuitenkin lisää huippunopeutta.

• Johdannaisosa: Johdannaisosa vähentää ylikulkua ja asettumisaikaa. Tämä tarkoittaa, että järjestelmän ohimenevä tila vaimenee enemmän. Lisäksi järjestelmä saavuttaa vakaan tilansa lyhyessä ajassa. Sillä ei kuitenkaan ole vaikutusta nousuaikaan tai vakaan tilan virheeseen.

• Kiinteä osa: Kiinteä osa lyhentää nousuaikaa ja eliminoi täysin vakaan tilan virheen. Se kuitenkin lisää piikin ylitystä ja asettumisaikaa.

• Viritys: Hyvällä ohjausjärjestelmällä on alhainen nousuaika, asettumisaika, huippunopeus ja vakaan tilan virhe. Siksi Kp, Kd, Ki on viritettävä lopullisesti säätämään edellä mainittujen tekijöiden vaikutusta hyvän valvontajärjestelmän saamiseksi.

Liitteenä on kuva, joka näyttää eri parametrien muuttamisen vaikutuksen PID -algoritmissa.

Vaihe 3: Itsetasapainottava robotti

Itsetasapainottava robotti on monikerroksinen kaksipyöräinen robotti.

Robotti yrittää tasapainottaa itsensä käyttäessään epätasaista voimaa. Se tasapainottaa itsensä käyttämällä voimaa, joka vastustaa robottiin kohdistuvien voimien seurausta.

Itsetasapainon menetelmät

Robotteja voidaan tasapainottaa neljällä tavalla. Nämä ovat seuraavat:

Tasapainotus kahdella IR -kallistusanturilla

Tämä on yksi rajuimmista tavoista tasapainottaa robotti, koska se vaatii hyvin vähän laitteistoa ja suhteellisen helppoa algoritmia. Tässä lähestymistavassa käytetään kahta kallistettua IR -anturia maan ja robotin välisen etäisyyden mittaamiseen. Lasketun etäisyyden perusteella PID: tä voidaan käyttää moottorien käyttämiseen robotin tasapainottamiseksi vastaavasti. Yksi tämän menetelmän haittapuoli on, että IR -anturi voi menettää joitain lukemia. Toinen ongelma on se, että etäisyyden laskemiseen tarvitaan keskeytys ja silmukat, mikä lisää algoritmin ajan monimutkaisuutta. Näin ollen tämä robotin tasapainotusmenetelmä ei ole kovin tehokas.

Tasapainotus kiihtyvyysanturin avulla

Kiihtyvyysmittari antaa meille kehon kiihtyvyyden kolmella akselilla. Y-akselilla (ylöspäin) ja x-akselilla (eteenpäin) suuntautuva kiihtyvyys antaa meille mittan painovoiman suunnan laskemiseksi ja siten kallistuskulman laskemiseksi. Kulma lasketaan seuraavasti:

θ = arctan (Ay/Ax) (1.2)

Tämän menetelmän käytön haittana on, että robotin liikkeen aikana myös vaakasuora kiihtyvyys lisätään lukemiin, mikä on suurtaajuista kohinaa. Näin ollen kallistuskulma on epätarkka.

Tasapainotus gyroskoopilla

Gyroskooppia käytetään laskemaan kulmanopeudet kolmella akselilla. Kallistuskulma saadaan käyttämällä seuraavaa yhtälöä.

θp (i) = θp (i − 1) + 1/6 (vali − 3 + 2vali − 2 + 2vali − 1 + vali) (1.3)

Yksi gyroskoopin käytön suuri haitta on se, että siinä on pieni DC -esijännite, joka on matalataajuinen kohina ja muutaman minuutin kuluttua palautetut arvot ovat täysin vääriä. Tämä aiheuttaa integroinnin jälkeen nollapisteen ajautumisen pois. Tämän seurauksena robotti pysyy pystysuorassa asennossa jonkin aikaa ja putoaa kaatumisen jälkeen.

Tasapainotus sekä kiihtyvyysanturilla että gyroskoopilla

Kuten edellä keskusteltiin, vain kiihtyvyysanturin tai gyroskoopin käyttö ei anna meille oikeaa kallistuskulmaa. Tämän vuoksi käytetään sekä kiihtyvyysanturia että gyroskooppia. Molemmat on upotettu MPU6050: een. Tässä saamme tiedot molemmilta ja sulautamme ne sitten käyttämällä Kalman -suodatinta tai täydentävää suodatinta.

• Kalman -suodatin: Kalman -suodatin laskee parhaan arvion dynaamisen järjestelmän tilasta meluisista mittauksista ja minimoi estimaatin keskimääräisen neliövirheen. Se toimii kahdessa vaiheessa, ennustaminen ja korjaus, kun otetaan huomioon järjestelmän dynamiikkaa kuvaavat erilliset stokastiset yhtälöt. Se on kuitenkin erittäin monimutkainen algoritmi, joka voidaan toteuttaa erityisesti mikro -ohjaimen rajoitetulla laitteistolla.

• Täydentävä suodatin: Tämä algoritmi käyttää ensisijaisesti gyroskoopista saatuja tietoja ja integroi ne ajan myötä saadakseen kallistuskulman. Se käyttää myös pientä osaa kiihtyvyysmittarin lukemista. Täydentävä suodatin minimoi itse asiassa kiihtyvyysmittarin korkeataajuisen kohinan ja gyroskoopin matalataajuisen kohinan ja sulauttaa ne sitten antamaan parhaan tarkan kallistuskulman.

Vaihe 4: Robotin suunnittelu

Olemme suunnitelleet itsetasapainottavan robotin käyttämällä MPU6050: tä täydentävän suodattimen toteuttamaa suhteellista johdannaissäädintä. Tämä pieni itsetasapainottavan robotin malli havainnollistaa meitä ohjausjärjestelmien hyödyllisyydestä robottien itsetasapainottamisessa.

Järjestelmän toteutus:

Järjestelmä on itsetasapainottava robotti. Se toteutetaan käyttämällä PID -ohjainta, joka on suhteellinen integroitu johdannaissäädin. Tasapainotamme robottia ajamalla sen pyöriä putoamisen suuntaan. Tätä tehdessä pyrimme pitämään robotin painopisteen kääntöpisteen yläpuolella. Jotta voisimme ajaa pyöriä kaatumisen suuntaan, meidän pitäisi tietää, mihin robotti putoaa ja kuinka nopeasti se putoaa. Nämä tiedot saadaan MPU6050: llä, jossa on kiihtyvyysmittari ja gyroskooppi. MPU6050 mittaa kallistuskulman ja antaa tehonsa mikro-ohjaimelle. MPU6050 on liitetty STM -korttiin I2C: n kautta. I2C: ssä yksi johto on kellolle, joka on nimeltään SCL. Toinen on tarkoitettu tiedonsiirtoon, joka on SDA. Tässä käytetään master -slave -kommunikaatiota. Aloitusosoite ja loppuosoite on määritetty tietämään, mistä tiedot alkavat ja mihin ne päättyvät. Olemme ottaneet käyttöön täydentävän suodattimen MPU6050: lle, joka on matematiikan suodatin kiihtyvyysanturin ja gyroskoopin lähtöjen yhdistämiseksi. Saatuaan tiedot MPU6050 -laitteesta mikro -ohjain suorittaa laskutoimituksia tietääkseen, mihin se putoaa. Laskelmien perusteella STM-mikro-ohjain antaa moottorinkuljettajalle komentoja ajaa ajoneuvoja putoamissuuntaan, mikä tasapainottaa robotin.

Vaihe 5: Projektin osat

Seuraavia komponentteja käytettiin itsetasapainotusrobottiprojektissa:

STM32F407

ST Microelectronicsin suunnittelema mikro-ohjain. Se toimii ARM Cortex-M -arkkitehtuurissa.

Moottorin ohjain L298N

Tätä IC: tä käytetään moottorin käyttämiseen. Se saa kaksi ulkoista tuloa. Yksi mikrokontrollerista, joka toimittaa sille PWM -signaalin. Pulssin leveyttä säätämällä moottorin nopeutta voidaan säätää. Sen toinen tulo on moottorin käyttämiseen tarvittava jännitelähde, joka on tapauksessamme 12 V: n akku.

DC -moottori

Tasavirtamoottori toimii tasavirtalähteellä. Tässä kokeessa DC -moottori pyörii moottorin ohjaimeen kytkettyjen optoerottimien avulla. Moottorin käyttämiseen olemme käyttäneet moottorikäyttöä L298N.

MPU6050

MPU6050: tä käytetään hakemaan tietoa siitä, mihin robotti putoaa. Se mittaa kaltevuuskulman suhteessa nollapisteeseen, joka on MPU6050: n asema, kun ohjelma käynnistyy.

MPU6050: ssä on 3-akselinen kiihtyvyysanturi ja 3-akselinen gyroskooppi. Kiihtyvyysmittari mittaa kiihtyvyyttä kolmea akselia pitkin ja gyroskooppi mittaa kulmanopeutta kolmen akselin ympäri. Jotta voimme yhdistää tuotoksen, meidän on suodatettava molempien äänet. Äänien suodattamiseksi meillä on Kalman ja täydentävä suodatin. Olemme ottaneet projektissamme käyttöön täydentävän suodattimen.

Optopari 4N35

Optoerotin on laite, jota käytetään eristtämään piirin pienjänniteosa ja suurjänniteosa. Kuten nimestä voi päätellä, se toimii valon perusteella. Kun pienjänniteosa saa signaalin, virta virtaa suurjänniteosassa

Vaihe 6: Robotin rakenne

Robotin rakenne selitetään seuraavasti:

Fyysinen rakenne

Itsetasapainottava robotti koostuu kahdesta kerroksesta, jotka koostuvat läpinäkyvästä muovista. Kahden kerroksen tiedot on esitetty alla:

Ensimmäinen kerros

Ensimmäisen kerroksen alaosaan olemme asettaneet solun virtalähteeksi STM -kortille. Molemmille puolille on sijoitettu myös kaksi 4 voltin moottoria kumpaankin, ja renkaat on kytketty robotin liikkumista varten. Ensimmäisen kerroksen yläosaan on asennettu kaksi 4 voltin paristoa (yhteensä 8 volttia) ja moottorin ohjainpiiri (L298N) moottorien käyttöä varten.

Toinen kerros

Robotin ylemmässä kerroksessa olemme asettaneet STM -levyn Perf Boardille. Toinen 4 opto -liittimen perf -levy asetetaan yläkerrokseen. Gyroskooppi asetetaan myös robotin yläkerrokseen alapuolelta. Molemmat komponentit on sijoitettu keskiosaan niin, että painopiste pidetään mahdollisimman alhaalla.

Robotin painopiste

Painopiste pidetään mahdollisimman alhaalla. Tätä tarkoitusta varten olemme asettaneet raskaita paristoja pohjakerrokseen ja kevyitä komponentteja, kuten STM -levyä ja optoerottimia yläkerrokseen.

Vaihe 7: Koodi

Koodi on koottu Atollic TrueStudioon. STM -studiota käytettiin virheenkorjaustarkoituksiin.

Vaihe 8: Johtopäätös

Monien kokeilujen ja havaintojen jälkeen tulemme lopulta siihen pisteeseen, jossa teemme yhteenvedon tuloksistamme ja keskustelemme siitä, kuinka pitkälle olemme onnistuneet toteuttamaan ja kehittämään järjestelmän tehokkuutta.

Yleiskatsaus

Kokeilun aikana moottorin nopeutta hallittiin onnistuneesti PID -algoritmilla. Käyrä ei kuitenkaan ole aivan tasainen suora. Siihen on monia syitä:

• Vaikka anturi on kytketty alipäästösuodattimeen, se tarjoaa edelleen tiettyjä lopullisia poistoja; nämä johtuvat epälineaarisista vastuksista ja joistakin väistämättömistä syistä analogiselle elektroniikalle.

• Moottori ei pyöri tasaisesti pienjännitteellä tai PWM: llä. Se tarjoaa nykäyksiä, jotka voivat aiheuttaa joitain vääriä arvoja, jotka syötetään järjestelmään.

• Havahtelun vuoksi anturi saattaa menettää joitakin rakoja, jotka antavat suurempia arvoja. • Toinen merkittävä syy virheisiin voi olla STM -mikrokontrollerin ydin kellotaajuus. Tämä STM -mikrokontrollerin malli tarjoaa 168 MHz: n ydinkellon. Vaikka tätä ongelmaa käsiteltiin tässä projektissa, tästä mallista on yleinen käsitys, että se ei tarjoa täsmälleen niin suurta taajuutta.

Avoimen silmukan nopeus tarjoaa erittäin tasaisen linjan, jossa on vain muutamia odottamattomia arvoja. PID -algoritmi toimii myös, mikä tarjoaa erittäin lyhyen moottorin asettumisajan. Moottorin PID -algoritmia testattiin eri jännitteillä pitäen vertailunopeus vakiona. Jännitteen muutos ei muuta moottorin nopeutta, mikä osoittaa, että PID -algoritmi toimii

Tehokkuus

Tässä keskustelemme kokeilun aikana havaitsemamme PID -säätimen tehokkuudesta.

Yksinkertainen toteutus

Olemme nähneet kokeilu- ja havainto -osiossa, että PID -säädin on erittäin helppo toteuttaa. Se vaatii vain kolme parametria tai vakioita, jotka on asetettava nopeudenohjausjärjestelmän saamiseksi

Verraton tehokkuus lineaarisille järjestelmille

Lineaarinen PID -säädin on tehokkain ohjainperheessä, koska logiikka on hyvin yksinkertainen ja sovellus on laajalle levinnyt lineaaristen tai melko lineaaristen sovellusten tapauksessa.

Rajoitukset

Selitimme abstraktisti tämän järjestelmän rajoituksista. Tässä keskustelemme muutamista niistä, joita havaitsimme.

Vakioiden valinta

Olemme nähneet, että vaikka PID -säädin on helppo toteuttaa, järjestelmän suuri haitta on kuitenkin se, että vaihe vakioiden arvon valitsemiseksi on työläs; koska on tehtävä erilaisia laskelmia. Toinen tapa on osuma- ja kokeilumenetelmä, mutta se ei myöskään ole tehokas.

Vakiot eivät aina ole vakioita

Kokeelliset tulokset osoittivat, että moottorin vertailunopeuden eri arvoille PID -säädin toimi virheellisesti samoilla PID -vakioiden arvoilla. Eri nopeuksille vakiot oli valittava eri tavalla, mikä lisää laskennallisia kustannuksia eksponentiaalisesti.

Ei -lineaarinen

Meidän tapauksessamme käytetty PID -säädin on lineaarinen, joten sitä voidaan soveltaa vain lineaarisiin järjestelmiin. Epälineaarisissa järjestelmissä ohjain on toteutettava eri tavalla. Vaikka käytettävissä on erilaisia epälineaarisia PID -menetelmiä, ne edellyttävät useampien parametrien valintaa. Tämä tekee järjestelmästä jälleen ei -toivotun korkeiden laskennallisten kustannusten vuoksi.

Ensimmäinen työntö vaaditaan

Kokeiluosassa osoitimme, että melko pienellä vertailunopeudella, jossa virhe on melko pieni alussa, PID: n toimittama PWM on niin pieni, että se ei luo vaadittua moottorin käynnistysmomenttia. Joten moottori ei käy joissakin kokeissa tai toisissa kokeissa tarjoaa suuren ylityksen ja pidemmän asettumisajan.

Vaihe 9: Erityinen kiitos

Erityiset kiitokset ryhmäni jäsenille, jotka auttoivat minua tässä projektissa.

Lähetän linkin videoon pian.

Toivottavasti pidät tätä opettavaista mielenkiintoisena.

Tämä on Tahir Ul Haq UET: stä. Kippis !!!